Алгоритм Кули — Тьюки

Схема общего алгоритма Кули — Тьюки

Для произвольного натурального числа ${\displaystyle N}$ дискретным преобразованием Фурье комплексного вектора ${\displaystyle x(j)}$, где ${\displaystyle j=0,\ldots ,N-1}$, называется комплексный вектор ${\displaystyle X(k)}$, где ${\displaystyle k=0,\ldots ,N-1}$, компоненты которого задаются формулой

${\displaystyle X(k)=\sum \limits _{j=0}^{N-1}x(j)\omega ^{kj},\;k=0,\ldots ,N-1,}$

где ${\displaystyle \omega =e^{-{\frac {2\pi i}{N}}}}$.

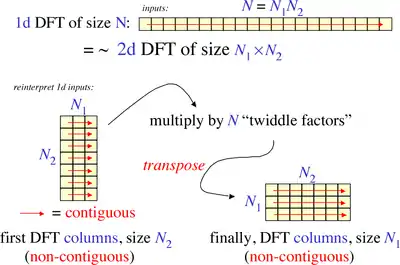
Для построения алгоритма делается предположение, что ${\displaystyle N=N_{1}N_{2}}$ для некоторых натуральных ${\displaystyle N_{1}}$ и ${\displaystyle N_{2}}$ и производится следующая замена индексов[1]:

${\displaystyle {\begin{array}{lll}&j=j_{1}+N_{1}j_{2},\ &j_{1}=0,\ldots ,N_{1}-1,\ &j_{2}=0,\ldots ,N_{2}-1,\\&k=k_{2}+N_{2}k_{1},\ &k_{1}=0,\ldots ,N_{1}-1,\ &k_{2}=0,\ldots ,N_{2}-1,\end{array}}}$

в результате которой получается

${\displaystyle X(k_{2}+N_{2}k_{1})=\sum \limits _{j_{1}=0}^{N_{1}-1}\sum \limits _{j_{2}=0}^{N_{2}-1}x(j_{1}+N_{1}j_{2})\omega ^{(j_{1}+N_{1}j_{2})(k_{2}+N_{2}k_{1})}.}$

Далее векторы входных и выходных данных преобразуются в двумерные массивы ${\displaystyle x'}$ и ${\displaystyle X'}$, задающиеся равенствами

${\displaystyle {\begin{array}{lll}&x'(j_{1},j_{2})=x(j_{1}+N_{1}j_{2}),\ &j_{1}=0,\ldots ,N_{1}-1,\ &j_{2}=0,\ldots ,N_{2}-1,\\&X'(k_{1},k_{2})=X(k_{2}+N_{2}k_{1}),\ &k_{1}=0,\ldots ,N_{1}-1,\ &k_{2}=0,\ldots ,N_{2}-1.\end{array}}}$

Стоит заметить, что компоненты ${\displaystyle X}$ упорядочены не так, как компоненты ${\displaystyle x}$.

Далее пусть ${\displaystyle \omega ^{N_{1}}=\gamma }$ и ${\displaystyle \omega ^{N_{2}}=\beta }$. Очевидно, что ${\displaystyle \omega ^{N_{1}N_{2}j_{2}k_{1}}=1}$. Тогда в терминах двумерных переменных формула преобразуется к виду[2]

${\displaystyle X'(k_{1},k_{2})=\sum \limits _{j_{1}=0}^{N_{1}-1}\beta ^{j_{1}k_{1}}\left(\omega ^{j_{1}k_{2}}\sum \limits _{j_{2}=0}^{N_{2}-1}x'(j_{1},j_{2})\gamma ^{j_{2}k_{2}}\right).}$

Таким образом, вычисление преобразования длины ${\displaystyle N=N_{1}N_{2}}$ сводится к выполнению следующих действий:

1. Вычисление ${\displaystyle N_{1}}$ преобразований длины ${\displaystyle N_{2}}$.
2. Умножение на комплексные «поворачивающие» множители.
3. Вычисление ${\displaystyle N_{2}}$ преобразований длины ${\displaystyle N_{1}}$.

При этом вместо ${\displaystyle N^{2}}$ комплексных сложений и ${\displaystyle N^{2}}$ комплексных умножений исходной формулы итоговая схема содержит не более ${\displaystyle N(N_{1}+N_{2}-2)}$ комплексных сложений и ${\displaystyle N(N_{1}+N_{2}+1)}$ комплексных умножений[2].

Каждое из преобразований длины ${\displaystyle N_{1}}$ или ${\displaystyle N_{2}}$ можно вычислять с помощью различных быстрых алгоритмов, в частности, снова по вышеприведённой схеме. В этом случае преобразование длины ${\displaystyle N=\prod \limits _{i=1}^{n}N_{i}}$ может быть представлено в форме, требующей выполнения ${\displaystyle N\sum \limits _{i=1}^{n}N_{i}}$ комплексных умножений[3].

Во многих приложениях длина преобразования равна степени двойки: ${\displaystyle N=2^{m}}$. Тогда в вышеприведённой схеме возможны варианты ${\displaystyle N_{1}=2}$ или ${\displaystyle N_{2}=2}$. В этом случае говорят об алгоритме Кули — Тьюки по основанию два[3] (англ. radix-2).

Если ${\displaystyle N_{1}=2}$, то говорят об алгоритме Кули — Тьюки с прореживанием по времени[3]. В этом случае уравнения преобразуются к виду

${\displaystyle {\begin{array}{rcl}X(k)&=&\sum \limits _{j=0}^{N/2-1}x(2j)\omega ^{2kj}+\omega ^{k}\sum \limits _{j=0}^{N/2-1}x(2j+1)\omega ^{2kj}\\X(k+N/2)&=&\sum \limits _{j=0}^{N/2-1}x(2j)\omega ^{2kj}-\omega ^{k}\sum \limits _{j=0}^{N/2-1}x(2j+1)\omega ^{2kj},\ k=0,\ldots ,N/2-1.\end{array}}}$

Схема реализации операции «бабочки»

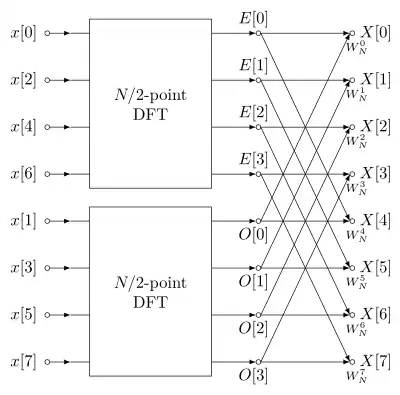
Если ввести обозначения ${\displaystyle E(k)=\sum \limits _{j=0}^{N/2-1}x(2j)\omega ^{2kj}}$ и ${\displaystyle O(k)=\sum \limits _{j=0}^{N/2-1}x(2j+1)\omega ^{2kj}}$, то уравнения можно переписать как

${\displaystyle {\begin{array}{rcl}X(k)&=&E(k)+\omega ^{k}O(k)\\X(k+N/2)&=&E(k)-\omega ^{k}O(k),\ k=0,\ldots ,N/2-1.\end{array}}}$

Такая операция обычно называется «бабочкой».

Данная процедура может быть применена к входному вектору рекурсивно. На каждом шаге ${\displaystyle N}$-точечное преобразование разбивается на два ${\displaystyle (N/2)}$-точечных преобразования, которые, в свою очередь, разбиваются таким же образом до тех пор, пока длина преобразования не станет равна единице. Затем происходит обратный ход, на каждом шаге длины результатов преобразований удваиваются с помощью «бабочек». При такой реализации выполняется ${\displaystyle (N/2)\log _{2}N}$ комплексных умножений и ${\displaystyle N\log _{2}N}$ комплексных сложений.

Этот процесс является примером применения методики «разделяй и властвуй». При этом во многих реализациях прямой рекурсии избегают и вместо неё дерево вычислений проходится в порядке поиска в ширину.

Если ${\displaystyle N_{2}=2}$, то говорят об алгоритме Кули — Тьюки с прореживанием по частоте[4]. В этом случае уравнения преобразуются к виду

${\displaystyle {\begin{array}{rcl}X(2k)&=&\sum \limits _{j=0}^{N/2-1}{\bigg (}x(j)+x(j+N/2){\bigg )}\omega ^{2kj},\\X(2k+1)&=&\sum \limits _{j=0}^{N/2-1}{\bigg (}x(j)-x(j+N/2){\bigg )}\omega ^{j(2k+1)},\ k=0,\ldots ,N/2-1.\end{array}}}$

Алгоритм и его рекурсивная реализация были изобретены около 1805 года К. Гауссом при интерполировании траекторий астероидов Паллада и Юнона[7]. Тогда открытие не получило широкого распространения и было опубликовано лишь после смерти учёного на новой латыни. Результат Гаусса несколько раз переоткрывался в различных формах в течение последующих 150 лет и стал популярным после публикации в 1965 году статьи Дж. Кули из IBM и Дж. Тьюки из Принстона, в которой алгоритм был в очередной раз переоткрыт, а также описывалась удобная реализация для ЭВМ[8].

Тот факт, что первооткрывателем алгоритма является Гаусс, был обнаружен лишь через несколько лет после публикации Кули и Тьюки. В своей статье они ссылались только на работу И. Дж. Гуда, в которой был описан алгоритм Гуда — Томаса.

Выражение преобразования Фурье длины ${\displaystyle N}$ через два преобразования длины ${\displaystyle N/2}$ иногда называют леммой Дэниэльсона — Ланцоша, так как оно было получено этими двумя авторами в 1942 году[9].

• Блейхут, Р.. Быстрые алгоритмы цифровой обработки сигналов (рус.). — М.: Мир, 1989. — 448 с.
• Нуссбаумер, Г. Быстрое преобразование Фурье и алгоритмы вычисления сверток. — М.: Радио и связь, 1985.
• Рабинер, Л., Гоулд, Б. Теория и применение цифровой обработки сигналов. — М.: Мир, 1978.

• Алгоритм Блуштайна