S-волна
S-волны представляют собой тип упругих волн. Название S-волны связано с английским «shear waves» — сдвиговые волны или волна сдвига (рисунок 1). Так как модуль сдвига в жидкостях и газах равен нулю, то S-волны могут проходить только через твёрдые тела. В случаях, когда упругость не проявляется (например, в несжимаемой жидкости), в них распространяются вязкие волны.

Основные свойства
Это поперечная волна, вектор её распространения перпендикулярен вектору поляризации. На рисунке 2 можно наблюдать поляризацию S-волны и видно, что из условия перпендикулярности вектору поляризации возникает два решения для волнового вектора для SH-волны и SV-волны, также там изображены и вектора распространения.
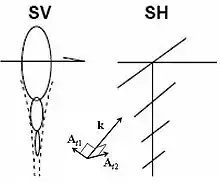
Уравнение на смещение для плоской гармонической волны SV, где А — амплитуда падающей волны:
Уравнение на смещение для плоской гармонической волны SH, где А — амплитуда падающей волны:
Скорость волн S в однородной изотропной среде выражается:
где — модуль сдвига (модуль жёсткости, иногда обозначается как G и также называется параметром Ламе), — плотность среды, через которую проходит волна. Из них видно, что скорость зависит от изменения μ.
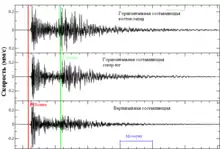
Типичные значения для скоростей S-волн во время землетрясений находятся в диапазоне от 2,5 до 5 км/с. Скорость поперечной волны всегда меньше скорости продольной волны, что видно на сейсмограммах (рисунок 3). В отличие от Р-волны, S-волна не может проходить через расплавленное внешнее ядро Земли, и это приводит к существованию теневой зоны для S-волн. Но они ещё могут появиться в твёрдом внутреннем ядре, так как возникают при преломлении Р-волны на границе расплавленного и твёрдого ядра, что называется разрывом Леманн, возникающие S-волны затем распространяются в твёрдой среде. И затем S-волны преломляются по границе, и они снова в свою очередь создают P-волны. Это свойство позволяет сейсмологам определять свойства внутреннего ядра.
Преломление S-волны на границе двух упругих сред
Для анализа волнового поля в реальных средах необходимо учитывать наличие границ между средами с разными упругими постоянными и свободную поверхность. На границе S двух однородных сред из условия отсутствия деформации получаем два непрерывных граничных условия
где n — вектор нормали к границе S. Первое выражение соответствует непрерывности вектора смещения, а второе отвечает за равенство давлений с обеих сторон и на границе. Так же как и для Р-волны, для волны типа SV существует 4 типа волн, порождаемых падением волны SV на поверхность двух сред — это две преломлённые Р, SV волны и две отражённые Р, SV волны, но для падающей на границу двух сред SH волны этого не происходит, она не порождает волны другого типа поляризации, что и видно на рисунках 4, 5.
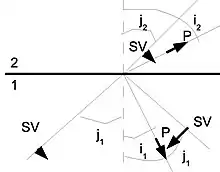
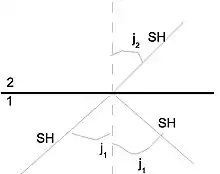
Преломление S-волны на границе среда-вакуум
В случае, когда упругая среда граничит с вакуумом, вместо двух условий остаётся только одно граничное условие, выражающее тот факт, что давление на границу со стороны вакуума должно равняться нулю:
Тогда в случае SV-волны, где А — это амплитуда падающей волны, — скорость поперечной волны в среде, — скорость продольной волны в среде, i — угол отражения моды P от моды SV, j — угол отражения моды SV от моды SV, получаем
— это коэффициент отражения моды SV от моды SV, — это коэффициент отражения моды P от моды SV. Напишем теперь коэффициент отражения в случае волны SH, где А — это амплитуда падающей волны, — скорость поперечной волны в среде, j — угол отражения моды SH от моды SH и — это коэффициент отражения SH в SH:
что говорит о том, что вся волна отражается при падении на свободную границу.
См. также
Литература
- Яновская Т. Б. Основы сейсмологии.-ВВМ, 2006
- Аки К.,Ричардс П. Количественная сейсмология: теория и методы.-М.:Мир,1983
- Сейсморазведка. Справочник геофизика./Под ред. И. И. Гурвича, В. П. Номоконова.- Москва: Недра,1981
