Эксетерская точка

Эксетерская точка — замечательная точка треугольника, обнаруженная на семинаре по вычислительной математике в Академии Филлипса в Эксетере в 1986 году, вошедшая в Энциклопедию центров треугольника как ${\displaystyle X(22)}$[1][1].

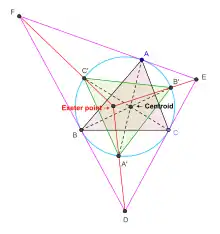
Определяется для треугольника ${\displaystyle \triangle ABC}$ следующим образом[1][2]: на описанной окружности отмечаются точки пересечения с медианами треугольника (${\displaystyle A'}$, ${\displaystyle B'}$ и ${\displaystyle C'}$ для медиан, проведённых через соответствующие вершины), строится треугольник, образованный касательными к описанной окружности в вершинах заданного треугольника (${\displaystyle \triangle DEF}$, где ${\displaystyle D}$ — вершина, противоположная стороне, образованной касательной в вершине ${\displaystyle A}$, ${\displaystyle E}$ — противоположная стороне, образованной касательной в ${\displaystyle B}$), в результате прямые, проходящие через ${\displaystyle DA'}$, ${\displaystyle EB'}$ и ${\displaystyle FC'}$ оказываюся пересекающимися, и образуют эксетерскую точку. Иными словами, эксетерская точка — точка пересечения 3 прямых, проходящих через 3 пары точек: через вершину тангенциального треугольника и через соответствующую ей точку пересечения медианы с описанной окружностью исходного треугольника.

Находится на прямой Эйлера.

Трилинейные координаты: ${\displaystyle (a\cdot (b^{4}+c^{4}-a^{4}),\,b\cdot (c^{4}+a^{4}-b^{4}),\,c\cdot (a^{4}+b^{4}-c^{4}))}$.