Число пересечений графа

Число пересечений графа — наименьшее число элементов в представлении данного графа как графа пересечений конечных множеств, или, эквивалентно, наименьшее число клик, необходимых для покрытия всех рёбер графа[1][2][3].

Не следует путать с минимальным числом пересечений рёбер графа.

Графы пересечений

Пусть F — семейство множеств (позволяется повторение множеств в F). Тогда граф пересечений F — это неориентированный граф, имеющий по вершине для каждого члена F и по ребру между любыми двумя множествами, имеющими непустое пересечение. Любой граф может быть представлен как граф пересечений[4]. Число пересечений графа — это наименьшее число k, такое, что существует представление такого типа, для которого объединение множеств F имеет k элементов[1]. Задача нахождения представления в виде графа пересечений с заданным числом элементов известна как задача нахождения базиса графа пересечений[5].

Покрытия рёбер кликами
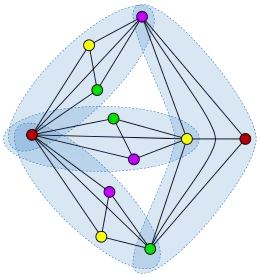
Граф с числом пересечений четыре. Четыре выделенные области показывают клики, покрывающие все рёбра графа.

Альтернативное определение числа пересечений графа G — это наименьшее число клик в G (полных подграфов графа G), которые покрывают все рёбра G [1][6]. Множество клик с таким свойством называется покрытием рёбер кликами, а потому число пересечений иногда называют числом покрытия рёбер кликами[7].

Равенство числа пересечений и числа покрытия рёбер кликами доказывается «прямолинейно». В одном направлении, предположим, что G является графом пересечений семейства F множеств, объединение U которых имеет k элементов. Тогда для любого элемента x из U подмножество вершин графа G, соответствующих множествам, содержащим x, образуют клику — любые две вершины этого подмножества смежны, поскольку их соответствующие множества имеют непустое пересечение, содержащее x. Далее — любое ребро в G содержится в одной из таких клик, поскольку ребро соответствует непустому пересечению, а пересечение не пусто, если оно содержит по меньшей мере один элемент U. Таким образом, рёбра графа G могут быть покрыты k кликами, по одной для каждого элемента U. В другом направлении, если граф G можно покрыть k кликами, то каждая вершина графа G может быть представлена множеством клик, содержащих вершину[8].

Верхние границы

Очевидно, что граф с m рёбрами имеет число пересечений, не превосходящее m — любое ребро образует клику, и эти клики вместе покрывают все рёбра[9].

Также верно, что любой граф с n вершинами имеет число пересечений, не превосходящее n2/4. Более строго, рёбра любого графа с n вершинами могут быть разделены максимум на n2/4 клик, которые являются либо отдельными рёбрами, либо треугольниками[2][8]. Это обобщает теорему Мантеля, утверждающую, что граф без треугольников имеет не более n2/4 рёбер. Для графов без треугольников оптимальное кликовое покрытие рёбер имеет клику для каждого ребра, а потому число пересечений равно числу рёбер[2].

Даже более сильное ограничение возможно, если число рёбер строго больше n2/4. Пусть p равно числу пар вершин, не соединённых рёбрами заданного графа G, и пусть t равно числу, для которого t(t − 1) ≤ p < t(t + 1). Тогда число пересечений графа G не превосходит p + t [2][10].

Графы, являющиеся дополнениями разреженных графов, имеют небольшое число пересечений — число пересечений любого графа G с n вершинами i не превосходит 2e2(d + 1)2ln n, где e — основание натурального логарифма, d максимальная степень дополнительного графа G [11].

Вычислительная сложность

Проверка, что у данного графа G число пересечений не превосходит заданного числа k, является NP-полной задачей[12][13][14]. Таким образом, является NP-трудной задачей вычисление числа пересечений заданного графа.

Задача вычисления числа пересечений, однако, является фиксированно-параметрически разрешимой. То есть существует функция f такая, что при равенстве числа пересечений числу k время вычисления этого числа не превосходит произведения f(k) на полином от n. Это можно показать, если обратить внимание на то, что существует не более 2k различных закрытых окрестностей в графе. Две вершины, принадлежащие одному и тому же набору клик, имеют одних и тех же соседей, а тогда граф, образованный выбором одной вершины для каждой закрытой окрестности, имеет то же самое число пересечений, что и исходный граф. Поэтому за полиномиальное время вход может быть сведён к меньшему ядру с максимум 2k вершинами. Применение алгоритма поиска с возвратом с экспоненциальным временем работы для этого ядра приводит к функции f, которая является двойной экспонентой от k [15]. Двойная экспоненциальная зависимость от k не может быть сведена к простой экспоненциональной зависимости посредством выделения ядра полиномиального размера, пока полиномиальная иерархия не исчезнет[16], и если гипотеза об экспоненциальном времени верна, двойной экспонециальной зависимости не избежать, будем мы использовать выделение ядра или нет[17].

Более эффективные алгоритмы известны для определённых специальных классов графов. Число пересечений интервального графа всегда равно числу максимальных клик графа, которое можно вычислить за полиномиальное время[18][19]. Более обще — число пересечений хордальных графов может быть вычислено алгоритмом, который строит порядок исключения вершин графа. На каждом шаге для каждой вершины v образуем клику для вершины v и её соседей и исключаем вершину, если остаются рёбра, инцидентные v, но ещё не покрытые кликами[19].

См. также

Примечания
  1. Gross, Yellen, 2006, с440.
  2. Roberts, 1985, с. 93–109.
  3. В. П. Козырев, С. В. Юшманов. Представления графов и сетей (кодирование, укладки и вложения) // Итоги науки и техники. : Сер. Теор. вероятн. Мат. стат. Теор. кибернет.. — М.: ВИНИТИ, 1990. — Т. 27. — С. 148. — doi:10.1007/BF01097528.
  4. Marczewski, 1945, с. 303–307.
  5. Гэри, Джонсон, 1982, с. 256, Задача ТГ59.
  6. Erdős, Goodman, Pósa, 1966, с. 106–112.
  7. Michael, Quint, 2006, с. 1309–1313.
  8. Erdős, Goodman, Pósa, 1966, с. 106–112.
  9. Balakrishnan, 1997, с. 40.
  10. Lovász, 1968, с. 231–236.
  11. Alon, 1986, с. 201–206.
  12. Гэри, Джонсон, 1982, с. 256, ЗадачаProblem ТГ59.
  13. Orlin, 1977, с. 406–424.
  14. Kou, Stockmeyer, Wong, 1978, с. 135–139.
  15. Gramm, Guo, Hüffner, Niedermeier, 2009, с. 2–15.
  16. Cygan, Kratsch, Pilipczuk, Pilipczuk, Wahlström, 2012, с. 254–265.
  17. Cygan, Pilipczuk, Pilipczuk, 2013.
  18. Opsut, Roberts, 1981, с. 479–492.
  19. Scheinerman, Trenk, 1999, с. 341–351.

Литература
  • Jonathan L. Gross, Jay Yellen. Graph Theory and its Applications. — CRC Press, 2006. — С. 440. — ISBN 978-1-58488-505-4.
  • Fred S. Roberts. Applications of edge coverings by cliques // Discrete Applied Mathematics. — 1985. — Т. 10, вып. 1. — С. 93—109. — doi:10.1016/0166-218X(85)90061-7.
  • E. Szpilrajn-Marczewski. Sur deux propriétés des classes d'ensembles // Fund. Math.. — 1945. — Т. 33. — С. 303—307.
  • Paul Erdős, A. W. Goodman, Lajos Pósa. The representation of a graph by set intersections // Canadian Journal of Mathematics. — 1966. — Т. 18, вып. 1. — doi:10.4153/CJM-1966-014-3.
  • T. S. Michael, Thomas Quint. Sphericity, cubicity, and edge clique covers of graphs // Discrete Applied Mathematics. — 2006. — Т. 154, вып. 8. — doi:10.1016/j.dam.2006.01.004.
  • V. K. Balakrishnan. Schaum's outline of theory and problems of graph theory. — McGraw-Hill Professional, 1997. — ISBN 978-0-07-005489-9.
  • László Lovász. Proceedings of the Colloquium held at Tihany, Hungary, 1966 / P. Erdős, G. Katona. — Academic Press, 1968. Как цитировано у Робертса (Roberts (1985))
  • Noga Alon. Covering graphs by the minimum number of equivalence relations // Combinatorica. — 1986. — Т. 6, вып. 3. — doi:10.1007/bf02579381.
  • J. B. Orlin. Contentment in graph theory: covering graphs with cliques // Proc. Kon. Ned. Acad. Wet.. — 1977. — Т. 80. — С. 406—424. — doi:10.1016/1385-7258(77)90055-5. Как процитировано у Робертса (Roberts (1985))
  • L. T. Kou, L. J. Stockmeyer, C. K. Wong. Covering edges by cliques with regard to keyword conflicts and intersection graphs // Communications of the ACM. — 1978. — Т. 21, вып. 2. — doi:10.1145/359340.359346.
  • Jens Gramm, Jiong Guo, Falk Hüffner, Rolf Niedermeier. Data reduction and exact algorithms for clique cover // Journal of Experimental Algorithmics. — 2009. — Т. 13, вып. 2. — doi:10.1145/1412228.1412236.
  • Marek Cygan, Stefan Kratsch, Marcin Pilipczuk, Michał Pilipczuk, Magnus Wahlström. Automata, Languages, and Programming: 39th International Colloquium, ICALP 2012, Warwick, UK, July 9-13, 2012, Proceedings, Part I / Artur Czumaj, Kurt Mehlhorn, Andrew Pitt, Roger Wattenhofer. — 2012. — Т. 7391. — (Lecture Notes in Computer Science). — ISBN 978-3-642-31593-0. — doi:10.1007/978-3-642-31594-7_22.
  • Marek Cygan, Marcin Pilipczuk, Michał Pilipczuk. Proc. 24th ACM-SIAM Symposium on Discrete Algorithms (SODA 2013). — 2013.
  • R. J. Opsut, F. S. Roberts. The Theory and Applications of Graphs / G. Chartrand, Y. Alavi, D. L. Goldsmith, L. Lesniak-Foster, D. R. Lick. — New York: Wiley, 1981.. Как процитировано у Робертса (Roberts (1985))
  • Edward R. Scheinerman, Ann N. Trenk. On the fractional intersection number of a graph // Graphs and Combinatorics. — 1999. — Т. 15, вып. 3. — doi:10.1007/s003730050068.
  • М. Гэри, Д. Джонсон. Вычислительные машины и труднорешаемые задачи. — М.: «Мир», 1982.

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.