Ханойская башня
Ханойская башня является одной из популярных головоломок XIX века. Даны три стержня, на один из которых нанизаны восемь колец, причём кольца отличаются размером и лежат меньшее на большем. Задача состоит в том, чтобы перенести пирамиду из восьми колец за наименьшее число ходов на другой стержень. За один раз разрешается переносить только одно кольцо, причём нельзя класть большее кольцо на меньшее.

История создания головоломки
Эту игру придумал французский математик Эдуард Люка в 1883 году[1], её продавали как забавную игрушку. Первоначально она называлась «Профессор Клаус (Claus) из Колледжа Ли-Су-Стьян (Li-Sou-Stian)»[1], но вскоре обнаружилось, что таинственный профессор из несуществующего колледжа — не более чем анаграмма фамилии изобретателя игры, профессора Люка (Lucas) из колледжа Сен-Луи (Saint Louis).

Решение
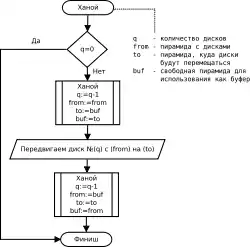
Существует несколько подходов к решению.
Рекурсивное решение
Рекурсивно решаем задачу «перенести башню из n−1 диска на 2-й штырь». Затем переносим самый большой диск на 3-й штырь, и рекурсивно решаем задачу «перенеси башню из n−1 диска на 3-й штырь».
Отсюда методом математической индукции заключаем, что минимальное число ходов, необходимое для решения головоломки, равно 2n − 1, где n — число дисков[2][3].
В информатике задачи, основанные на легенде о Ханойской башне, часто рассматривают в качестве примера использования рекурсивных алгоритмов и преобразования их к нерекурсивным.
«Треугольное» решение
Расположим штыри в виде треугольника. Начнём с самого маленького кольца и переложим его на любую отметку. В дальнейшем это кольцо нужно перемещать в том же направлении, что и при первом перекладывании. Затем перенесём какое-нибудь из оставшихся колец (такой ход единственный), после чего снова переложим самое маленькое кольцо и т. д. (Интересно заметить, что перенумеровав «кольца» по порядку, мы добьёмся неожиданного эффекта: чётные кольца будут перемещаться из одной вершины треугольника в другую в одном направлении, а нечётные — в противоположном направлении.)
Циклическое решение
Обозначим через «1-2» такое действие: переложить диск или с 1-го штыря на 2-й, или со 2-го на 1-й, в зависимости от того, где он меньше. Тогда, чтобы решить головоломку с чётным количеством дисков, надо многократно повторять действия: 1-2, 1-3, 2-3. Если число дисков нечётно — 1-3, 1-2, 2-3.
Применение кода Грея для решения
Код Грея, рефлексный двоичный код в двоичной системе счисления, в котором два соседних значения различаются только в одном двоичном разряде. Изначально код Грея предназначался для защиты от ложного срабатывания электромеханических переключателей. Сегодня коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления. Код получил имя исследователя лабораторий Bell Labs Фрэнка Грея. Он запатентовал (за номером 2632058) и использовал этот код в своей импульсной системе связи.
Коды Грея могут быть применены в решении задачи о Ханойских башнях.
Пусть N — количество дисков. Начнём с кода Грея длины N, состоящего из одних нулей (то есть G0), и будем двигаться по кодам Грея (от Gi переходить к Gi+1). Поставим в соответствие каждому i-ому биту текущего кода Грея i-ый диск (причём самому младшему биту соответствует наименьший по размеру диск, а самому старшему биту — наибольший). Поскольку на каждом шаге изменяется ровно один бит, то мы можем понимать изменение бита i как перемещение i-го диска. Заметим, что для всех дисков, кроме наименьшего, на каждом шаге имеется ровно один вариант хода (за исключением стартовой и финальной позиций). Для наименьшего диска всегда имеется два варианта хода, однако имеется стратегия правильного выбора хода: для нечётного N последовательность перемещений наименьшего диска f→t→r→f→t→r→… (где f — стартовый стержень, t — финальный стержень, r -оставшийся стержень), а для чётного f→r→t→f→r→t→….
Пример алгоритма решения на языке C++:
// Ханойские башни
#include <iostream>
using namespace std;
void hanoi_towers(int quantity, int from, int to, int buf_peg) //quantity-число колец, from-начальное положение колец(1-3),to-конечное положение колец(1-3)
{ //buf_peg - промежуточный колышек(1-3)
if (quantity != 0)
{
hanoi_towers(quantity-1, from, buf_peg, to);
cout << from << " -> " << to << endl;
hanoi_towers(quantity-1, buf_peg, to, from);
}
}
int main()
{
setlocale(LC_ALL,"rus");
int start_peg, destination_peg, buffer_peg, plate_quantity;
cout << "Номер первого столбика:" << endl;
cin >> start_peg;
cout << "Номер конечного столбика:" << endl;
cin >> destination_peg;
cout << "Номер промежуточного столбика:" << endl;
cin >> buffer_peg;
cout << "Количество дисков:" << endl;
cin >> plate_quantity;
hanoi_towers(plate_quantity, start_peg, destination_peg, buffer_peg);
return 0;
}
Пример алгоритма решения на языке Pascal:
program hanoibns(input,output);
var n:integer;
procedure tower(k:integer;a,b,c:char);
begin
if k>1 then tower(k-1,a,c,b);
writeln('from ',a,' to ',b);
if k>1 then tower(k-1,c,b,a)
end;
begin
read(n);
tower(n,'A','C','B')
end.
Пример алгоритма решения на языке Haskell:
hanoiSteps :: Int -> [(Int, Int)]
hanoiSteps n = step (max 0 n) 1 3 2 []
where
step 0 _ _ _ rest = rest
step n f t s rest = step (n - 1) f s t $ (f, t) : step (n - 1) s t f rest
Пример алгоритма решения на языке Python:
def Hanoi(n, A, C, B):
if (n != 0):
Hanoi(n - 1, A, B, C)
print ('Move the plate from', A, 'to', C)
Hanoi(n - 1, B, C, A)
Пример алгоритма решения на языке Java:
public class Hanoi {
public static void hanoiTowers(int quantity, int from, int to, int buf_peg) {
if (quantity != 0)
{
hanoiTowers(quantity-1, from, buf_peg, to);
System.out.println("" + from + " -> " + to );
hanoiTowers(quantity-1, buf_peg, to, from);
}
}
public static void main(String[] args) {
int start_peg = 1, destination_peg = 2, buffer_peg = 3, plate_quantity = 4;
hanoiTowers(plate_quantity, start_peg, destination_peg, buffer_peg);
}
}
Пример итеративного алгоритма решения на языке C
#include <stdio.h>
#include <math.h>
void carryingOver(int, int, int);
main()
{
int number, countDisk, counter = 1, count;
printf("Введите количество дисков: "); /* Ханойская башня */
scanf("%d", &number);
while (counter <= pow(2, number) - 1) { /* Запускаем цикл повторений */
if (counter % 2 != 0) { /* На нечетном ходу мы будем трогать только самый маленький диск */
printf("%3d %d ", counter, 1);
carryingOver(number, counter, 1); /* С помощью этой функции определяем для данного диска перемещение */
}
else { /* Определяем диск который нужно переместить на четном ходу */
count = counter;
countDisk = 0;
while (count % 2 == 0) { /* Диск который нужно переместить */
countDisk++; /* будет числом деления номера хода на 2 без остатка */
count = count / 2;
}
printf("%3d %d ", counter, countDisk + 1);
carryingOver(number, counter, countDisk + 1);
}
counter++;
}
return 0;
}
/* Функция определения перемещения дисков */
void carryingOver(int n ,int i, int k)
{
int t, axisX, axisY, axisZ;
if (n % 2 == 0) { /* Определяем порядок осей в зависимости от четности */
axisX = 1; /* и не четности количества дисков */
axisY = 2;
axisZ = 3;
}
else {
axisX = 1;
axisY = 3;
axisZ = 2;
}
/* Номер хода можно представить единственным образом */
/* как произведение некоего нечетного числа на степень двойки */
/* k будет номером диска который мы перемещаем */
t = ((i / pow(2, k - 1)) - 1) / 2;
if (k % 2 != 0) { /* Определяем перемещение дисков для нечетного хода */
switch (t % 3) { /* Выбираем перемещение в зависимости от данного условия */
case 0:
printf("%d -> %d\n", axisX, axisY);
break;
case 1:
printf("%d -> %d\n", axisY, axisZ);
break;
case 2:
printf("%d -> %d\n", axisZ, axisX);
break;
}
}
else { /* Определяем перемещение дисков для чётного хода */
switch (t % 3) {
case 0:
printf("%d -> %d\n", axisX, axisZ);
break;
case 1:
printf("%d -> %d\n", axisZ, axisY);
break;
case 2:
printf("%d -> %d\n", axisY, axisX);
break;
}
}
}
Существуют программы визуализации решения этой головоломки.
Варианты
С четырьмя и более стержнями
Хотя вариант с тремя стержнями имеет простое рекурсивное решение, оптимальное решение Ханойской башни с четырьмя стержнями долгое время являлось нерешённой проблемой.
Очевидно, что для любого количества стержней существует алгоритм для нахождения оптимальных решений, достаточно представить головоломку в виде неориентированного графа, сопоставив размещениям дисков вершины, а ходам — рёбра, и использовать любой алгоритм поиска (например, поиск в ширину) для нахождения оптимального решения. Однако эффективной стратегии определения оптимального решения для большого числа дисков нет: количество ходов, необходимое для решения головоломки с 10 стержнями и 1000 дисками, остаётся неизвестным.
Существует предположительно оптимальный алгоритм Фрейма — Стюарта, разработанный в 1941 году[4]. Связанная гипотеза Фрейма — Стюарта утверждает, что алгоритм Фрейма — Стюарта всегда находит оптимальное решение. Оптимальность алгоритма Фрейма — Стюарта была экспериментально проверена вплоть до 30 дисков на 4 стержнях[5]. В 2014 году было окончательно доказано, что для четырёх стержней Алгоритм Фрейма — Стюарта является оптимальным [6].
Другие варианты решения Ханойской башни с четырьмя стержнями рассматриваются в обзорной статье Пола Стокмайера[7].
Алгоритм Фрейма — Стюарта
Алгоритм Фрейма — Стюарта, дающий оптимальное решение для четырёх и предположительно оптимальное решение для большего количества стержней, описывается следующим образом:
- Пусть — количество дисков.
- Пусть — число стержней.
- Определим как наименьшее число ходов, необходимое для переноса n дисков с использованием r стержней.
Алгоритм может быть описан рекурсивно:
- Для некоторого , , перенести верхние на стержень i, не являющийся ни начальным, ни конечным стержнем, затратив на это ходов.
- Не используя стержень i, содержащий теперь верхние дисков, перенести оставшиеся дисков на конечный стержень, используя только оставшиеся стержней и затратив на это ходов.
- Наконец, переместить верхние дисков на конечный стержень, затратив на это ходов.
На весь процесс требуется ходов. Значение выбирается таким образом, чтобы значение этого выражения было минимальным. В случае 4 стержней, оптимальное равно , где - это функция ближайшего целого.[8]
Легенды
Придуманная профессором Люка легенда гласит, что в Великом храме города Бенарес, под собором, отмечающим середину мира, находится бронзовый диск, на котором укреплены 3 алмазных стержня, высотой в один локоть и толщиной с пчелу. Давным-давно, в самом начале времён, монахи этого монастыря провинились перед богом Брахмой. Разгневанный Брахма воздвиг три высоких стержня и на один из них возложил 64 диска, сделанных из чистого золота. Причём так, что каждый меньший диск лежит на большем.
Как только все 64 диска будут переложены со стержня, на который Брахма сложил их при создании мира, на другой стержень, башня вместе с храмом обратятся в пыль и под громовые раскаты погибнет мир.
Количество перекладываний в зависимости от количества колец вычисляется по формуле .
Число перемещений дисков, которые должны совершить монахи, равно 18 446 744 073 709 551 615. Если бы монахи, работая день и ночь, делали каждую секунду одно перемещение диска, их работа продолжалась бы почти 585 миллиардов лет.
В культуре
В рассказе Эрика Фрэнка Рассела «Ваш ход» (Now Inhale, в другом переводе — «Игра на выживание»)[9], чтобы оттянуть время казни инопланетянами, главный герой выбирает игру в Ханойскую башню с 64 дисками в качестве последней игры. Объявленные правила модифицированы для двух игроков — игроки должны перекладывать диски по одному за ход, победителем считается тот, кто сделает последний ход. Герой называет такую игру «арки-маларки» и клянётся, что «священнослужители Бенаресского храма» на Земле играют в эту игру.
В фильме «Восстание планеты обезьян» Ханойскую башню используют в качестве проверки интеллекта подопытных. Обезьяна собирает головоломку из четырёх колец за двадцать ходов.
Ханойская башня — одна из традиционных головоломок в видеоиграх канадской компании BioWare — в частности, «Jade Empire», «Star Wars: Knights of the Old Republic», «Mass Effect» и «Dragon Age: Inquisition». Встречаются они и в квесте Legend of Kyrandia II.
Примечания
- Мартин Гарднер, Математические головоломки и развлечения
- Petković, Miodrag. Famous Puzzles of Great Mathematicians (неопр.). — AMS Bookstore, 2009. — С. 197. — ISBN 0-8218-4814-3.
- Graham, Ronald. Concrete Mathematics: A Foundation for Computer Science (англ.). — Addison–Wesley, 1998. — P. 21. — ISBN 0201558025.
- Solution to advanced problem 3819, American Mathematical Monthly, 1941.
- Korf, Richard E., and Ariel Felner. Recent Progress in Heuristic Search: a Case Study of the Four-Peg Towers of Hanoi Problem (англ.) // IJCAI : journal. — 2007. — P. 2324—2329. Архивировано 24 сентября 2015 года.
- Bousch, T. La quatrieme tour de Hanoi (неопр.) // Bull. Belg. Math. Soc. Simon Stevin. — 2014. — Т. 21. — С. 895—912.
- Paul Stockmeyer. Variations on the Four-Post Tower of Hanoi Puzzle (неопр.) // Congressus Numerantium. — 1994. — Т. 102. — С. 3—12.
- University of Toronto CSC148 Slog (5 апреля 2014). Дата обращения: 22 июля 2015.
- Рассел, Эрик Фрэнк. Ваш ход // Если. — 1994. — Апрель. — С. 34—42.
См. также
Ссылки
- последовательность A007664 в OEIS
- Константин Кноп. Ханойская башня. Элементы (22 октября 2012).
- Онлайн-игра Ханойские башни