Функция Уолша

Функциями Уолша называется семейство функций, образующих ортогональную систему, принимающих значения только +1 и −1 на всей области определения.

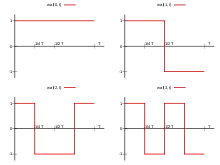
Графики первых четырёх функций Уолша

В принципе, функции Уолша могут быть представлены в непрерывной форме, но чаще их определяют как дискретные последовательности из $2^{n}$ элементов. Группа из $2^{n}$ функций Уолша образует матрицу Адамара.

Функции Уолша получили широкое распространение в радиосвязи, где с их помощью осуществляется кодовое разделение каналов (CDMA), например, в таких стандартах сотовой связи, как IS-95, CDMA2000 или UMTS.

Система функций Уолша является ортонормированным базисом и, как следствие, позволяет раскладывать сигналы произвольной формы в обобщённый ряд Фурье.

Обобщением функций Уолша на случай более чем двух значений являются функции Виленкина — Крестенсона.

Обозначение

Пусть функция Уолша определена на интервале [0, T]; за пределами этого интервала функция периодически повторяется. Введём безразмерное время $\theta =t/T$ . Тогда функция Уолша под номером k обозначается как $\operatorname {wal} (k,\theta )$ . Нумерация функций зависит от метода упорядочения функций. Существует упорядочение по Уолшу — в этом случае функции обозначаются так, как описано выше. Также распространены упорядочения по Пэли ( $\operatorname {pal} (p,\theta )$ ) и по Адамару ( $\operatorname {had} (h,\theta )$ ).

Относительно момента $\theta =0$ функции Уолша можно разделить на чётные и нечётные. Они обозначаются как $\operatorname {cal} (k,\theta )$ и $\operatorname {sal} (k,\theta )$ соответственно. Эти функции аналогичны тригонометрическим синусам и косинусам. Связь между этими функциями выражается следующим образом:

\operatorname {cal} (k,\theta )=\operatorname {wal} (2k,\theta ),

\operatorname {sal} (k,\theta )=\operatorname {wal} (2k-1,\theta ).

Формирование

Существует несколько способов формирования. Рассмотрим один из них, наиболее наглядный: матрица Адамара может быть сформирована рекурсивным методом с помощью построения блочных матриц по следующей общей формуле:

H_{2^{n}}={\begin{bmatrix}H_{2^{n-1}}&H_{2^{n-1}}\\H_{2^{n-1}}&-H_{2^{n-1}}\end{bmatrix}}.

Так может быть сформирована матрица Адамара длины $2^{n}$ :

H_{1}={\begin{bmatrix}1\end{bmatrix}},

H_{2}={\begin{bmatrix}1&1\\1&-1\end{bmatrix}},

H_{4}={\begin{bmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\end{bmatrix}},

H_{8}={\begin{bmatrix}1&1&1&1&1&1&1&1\\1&-1&1&-1&1&-1&1&-1\\1&1&-1&-1&1&1&-1&-1\\1&-1&-1&1&1&-1&-1&1\\1&1&1&1&-1&-1&-1&-1\\1&-1&1&-1&-1&1&-1&1\\1&1&-1&-1&-1&-1&1&1\\1&-1&-1&1&-1&1&1&-1\end{bmatrix}},

Каждая строка матрицы Адамара и является функцией Уолша.

В данном случае функции упорядочены по Адамару. Номер функции по Уолшу вычисляется из номера функции по Адамару путём перестановки битов в двоичной записи номера в обратном порядке с последующим преобразованием результата из кода Грея.

Пример

Номер по Уолшу	Двоичная форма	Преобразование из кода Грея	Перестановка бит	Номер по Адамару
0	000	000	000	0
1	001	001	100	4
2	010	011	110	6
3	011	010	010	2
4	100	110	011	3
5	101	111	111	7
6	110	101	101	5
7	111	100	001	1

В итоге получается матрица Уолша, в которой функции упорядочены по Уолшу:

W_{8}={\begin{bmatrix}1&1&1&1&1&1&1&1\\1&1&1&1&-1&-1&-1&-1\\1&1&-1&-1&-1&-1&1&1\\1&1&-1&-1&1&1&-1&-1\\1&-1&-1&1&1&-1&-1&1\\1&-1&-1&1&-1&1&1&-1\\1&-1&1&-1&-1&1&-1&1\\1&-1&1&-1&1&-1&1&-1\end{bmatrix}}.

Свойства

1. Ортогональность

Скалярное произведение двух разных функций Уолша равно нулю:

\int \limits _{0}^{1}\operatorname {wal} (n,\theta )\cdot \operatorname {wal} (k,\theta )\,d\theta =0\qquad {\text{при }}k\neq n.

Пример

Допустим, что n = 1, k = 3 (см. выше). Тогда

\int \limits _{0}^{1}\operatorname {wal} (1,\theta )\cdot \operatorname {wal} (3,\theta )\,d\theta =

=\int \limits _{0}^{1/4}1^{2}\,d\theta +\int \limits _{1/4}^{1/2}1\cdot (-1)\,d\theta +\int \limits _{1/2}^{3/4}(-1)\cdot 1\,d\theta +\int \limits _{3/4}^{1}(-1)^{2}\,d\theta =0.

2. Мультипликативность

Произведение двух функций Уолша даёт функцию Уолша:

\operatorname {wal} (n,\theta )\cdot \operatorname {wal} (k,\theta )=\operatorname {wal} (i,\theta ),

где $i=n\oplus k$ — сложение по модулю 2 номеров в двоичной системе.

Пример

Допустим, что n = 1, k = 3. Тогда

n\oplus k=01_{2}\oplus 11_{2}=10_{2}=2.

В результате умножения получим:

{\begin{array}{|c|c|c|c||c|}&&&&n\\\hline 1&1&-1&-1&\operatorname {wal} (1,\theta )\\1&-1&1&-1&\operatorname {wal} (3,\theta )\\\hline 1&-1&-1&1&\operatorname {wal} (2,\theta )\\\end{array}}

Преобразование Уолша — Адамара

Является частным случаем обобщённого преобразования Фурье, в котором базисом выступает система функций Уолша.

Обобщённый ряд Фурье представляется формулой

S(t)=\sum _{i=0}^{\infty }c_{i}\cdot u_{i}(t),

где $u_{i}$ это одна из базисных функций, а $c_{i}$ — коэффициент.

Разложение сигнала по функциям Уолша имеет вид

S(t)=\sum _{k=0}^{\infty }c_{k}\cdot \operatorname {wal} (k,t/T).

В дискретной форме формула запишется следующим образом:

S(n)=\sum _{k=0}^{\infty }c_{k}\cdot \operatorname {wal} (k,n).

Определить коэффициенты $c_{i}$ можно, осуществив скалярное произведение раскладываемого сигнала на соответствующую базисную функцию Уолша:

c_{k}={\frac {1}{T}}\int \limits _{0}^{T}S(t)\cdot \operatorname {wal} (k,t/T)\,dt.

Следует учитывать периодический характер функций Уолша.

Существует также быстрое преобразование Уолша[1]. Оно является в значительной степени более эффективным, чем преобразование Уолша — Адамара[2]. Кроме того, для частного случая с двумя переменными функции Уолша обобщены как поверхности[3]. Также существуют восемь аналогичных функциям Уолша базисов ортогональных бинарных функций[4], отличающихся нерегулярной структурой, которые также обобщены на случай функций двух переменных. Для каждого из восьми базисов доказано представление «ступенчатых» функций в виде конечной суммы бинарных функций, взвешиваемых с соответствующими коэффициентами[5].

Литература

Баскаков С. И. Радиотехнические цепи и сигналы. — М.: Высшая школа, 2005. — ISBN 5-06-003843-2.
Голубов Б. И., Ефимов А. В., Скворцов В. А. Ряды и преобразования Уолша: теория и применения. — М.: Наука, 1987.
Залманзон Л. А. Преобразования Фурье, Уолша, Хаара и их применение в управлении, связи и других областях. — М.: Наука, 1989. — ISBN 5-02-014094-5.

См. также

Примечания

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] БЫСТРОЕ ПРЕОБРАЗОВАНИЕ УОЛША. В. Н. Малозёмов.

[2] Fast Walsh Transform.

[3] Romanuke V. V. ON THE POINT OF GENERALIZING THE WALSH FUNCTIONS TO SURFACES.

[4] Romanuke V. V. GENERALIZATION OF THE EIGHT KNOWN ORTHONORMAL BASES OF BINARY FUNCTIONS TO SURFACES.

[5] Romanuke V. V. EQUIDISTANTLY DISCRETE ON THE ARGUMENT AXIS FUNCTIONS AND THEIR REPRESENTATION IN THE ORTHONORMAL BASES SERIES.