Функции параболического цилиндра

Фу́нкции параболи́ческого цили́ндра (функции Вебера) — общее название для специальных функций, являющихся решениями дифференциальных уравнений, получающихся при применении метода разделения переменных для уравнений математической физики, таких как уравнение Лапласа, уравнение Пуассона, уравнение Гельмгольца и др. в системе координат параболического цилиндра.

В общем случае функции параболического цилиндра — решения следующего уравнения

${\displaystyle {\frac {d^{2}f}{dz^{2}}}+\left(az^{2}+bz+c\right)f=0.\quad (1)}$

График функций Вебера с положительным целым индексом

При выполнении линейной замены переменной в этом уравнении получается уравнение:

${\displaystyle {\frac {d^{2}f}{dz^{2}}}+\left(\nu +{\frac {1}{2}}-{\frac {z^{2}}{4}}\right)f=0,}$

решения которого называются функциями Вебера и обозначаются ${\displaystyle D_{\nu }(z).}$

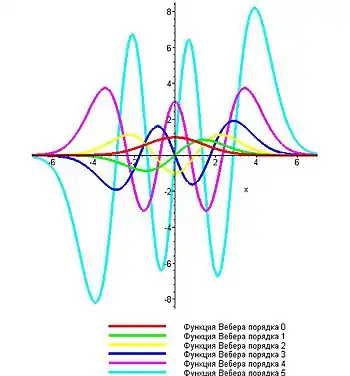
Функции ${\displaystyle D_{\nu }(z),D_{\nu }(-z),D_{-\nu -1}(iz),D_{-\nu -1}(-iz)}$ являются решениями уравнения Вебера, причём при нецелом ${\displaystyle \nu }$ функции ${\displaystyle D_{\nu }(z),D_{\nu }(-z)}$ линейно независимы. Для всех ${\displaystyle \nu }$ функции ${\displaystyle D_{\nu }(z),D_{-\nu -1}(\pm iz)}$ также линейно независимы.

График функций Эрмита с положительным индексом

График функций Эрмита с отрицательным целым индексом

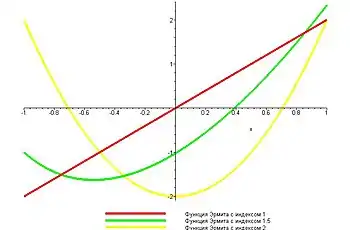
На практике часто пользуются и другими функциями параболического цилиндра — функциями Эрмита, являющихся решениями уравнения Эрмита, которое получается из ${\displaystyle (1)}$ заменой ${\displaystyle f(\alpha z+\beta )=e^{-z^{2}}y(z)}$

${\displaystyle {\frac {d^{2}y}{dz^{2}}}-2z{\frac {dy}{dz}}+2\nu y=0.\qquad (2)}$

Функции Эрмита обозначаются ${\displaystyle H_{\nu }(z).}$ Общее решение уравнения ${\displaystyle (2):}$

${\displaystyle y(z)=c_{1}H_{\nu }(z)+c_{2}\Phi \left(-{\frac {\nu }{2}};{\frac {1}{2}};z^{2}\right),}$

где ${\displaystyle \Phi \left(\alpha$ ;\beta ;z\right)} — вырожденная гипергеометрическая функция.

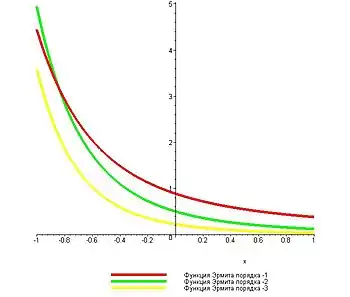
При целом неотрицательном ${\displaystyle \nu }$ функция Эрмита совпадает с полиномом Эрмита. При целом отрицательном ${\displaystyle \nu }$ функция Эрмита выражается в замкнутом виде через функцию ошибок.