Функции Крылова

Графики функций Крылова

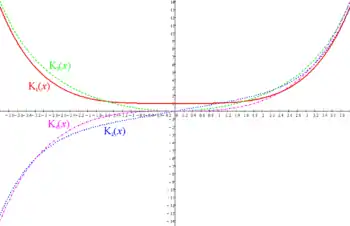
Функции Крылова выражаются следующим образом:[3]

${\displaystyle \operatorname {K} _{1}(x)={\frac {1}{2}}(\operatorname {ch} x+\cos x)}$,

${\displaystyle \operatorname {K} _{2}(x)={\frac {1}{2}}(\operatorname {sh} x+\sin x)}$,

${\displaystyle \operatorname {K} _{3}(x)={\frac {1}{2}}(\operatorname {ch} x-\cos x)}$,

${\displaystyle \operatorname {K} _{4}(x)={\frac {1}{2}}(\operatorname {sh} x-\sin x)}$.

Основное свойство функций Крылова в том, что производная от любой из них даёт предыдущую:

${\displaystyle \operatorname {K} _{1}(x)=\operatorname {K} _{2}'(x)=\operatorname {K} _{3}''(x)=\operatorname {K} _{4}'''(x)=\operatorname {K} _{1}^{IV}(x)}$.

Кроме того выполнены следующие начальные условия: при ${\displaystyle x=0}$, первая функция равна 1, а все остальные равны 0:

${\displaystyle \operatorname {K} _{1}(0)=1}$, ${\displaystyle \operatorname {K} _{2}(0)=\operatorname {K} _{3}(0)=\operatorname {K} _{4}(0)=0}$.

При ${\displaystyle a<0}$ решение уравнения (1) выражается через функции

${\displaystyle \operatorname {\Phi } _{1}(x)=\operatorname {ch} x\cdot \cos x}$,

${\displaystyle \operatorname {\Phi } _{2}(x)=\operatorname {sh} x\cdot \sin x}$,

${\displaystyle \operatorname {\Phi } _{3}(x)=\operatorname {sh} x\cdot \cos x}$,

${\displaystyle \operatorname {\Phi } _{4}(x)=\operatorname {ch} x\cdot \sin x}$,

которые называются функциями Крылова — Власова[4] в честь В.З. Власова. Общим решением уравнения (1) при ${\displaystyle a<0}$ является линейная комбинация четырёх функций ${\displaystyle \operatorname {\Phi } _{i}(\beta x)}$ (при ${\displaystyle i=1,2,3,4}$), где ${\displaystyle \beta ={\sqrt[{4}]{-a/4}}}$.

Чаще при решении задач используются различные комбинации функций Крылова — Власова, которые также называют функциями Крылова:[5][6]

${\displaystyle \operatorname {V} _{1}(x)=\operatorname {ch} x\cdot \cos x=\operatorname {\Phi } _{1}(x)}$,

${\displaystyle \operatorname {V} _{2}(x)={\frac {1}{2}}\left(\operatorname {ch} x\cdot \sin x+\operatorname {sh} x\cdot \cos x\right)={\frac {1}{2}}\left(\operatorname {\Phi } _{4}(x)+\operatorname {\Phi } _{3}(x)\right)}$,

${\displaystyle \operatorname {V} _{3}(x)={\frac {1}{2}}\operatorname {sh} x\cdot \sin x={\frac {1}{2}}\operatorname {\Phi } _{2}(x)}$,

${\displaystyle \operatorname {V} _{4}(x)={\frac {1}{4}}\left(\operatorname {ch} x\cdot \sin x-\operatorname {sh} x\cdot \cos x\right)={\frac {1}{4}}\left(\operatorname {\Phi } _{4}(x)-\operatorname {\Phi } _{3}(x)\right)}$.

Основные свойства функций Крылова в этом случае почти сохраняются:

${\displaystyle \operatorname {V} _{1}(x)=\operatorname {V} _{2}'(x)=\operatorname {V} _{3}''(x)=\operatorname {V} _{4}'''(x)=-{\frac {1}{4}}\operatorname {V} _{1}^{IV}(x)}$.

${\displaystyle \operatorname {V} _{1}(0)=1}$, ${\displaystyle \operatorname {V} _{2}(0)=\operatorname {V} _{3}(0)=\operatorname {V} _{4}(0)=0}$.

• Тригонометрические функции
• Гиперболические функции

• Крылов А.Н. О расчете балок, лежащих на упругом основании. Л.: АН СССР, 1931. 154 с