Фазовая диаграмма воды
Фа́зовая диагра́мма воды — графическое отображение равновесного состояния фаз воды (жидкости, водяного пара и различных модификаций льда). Строится в системе координат температура—давление.
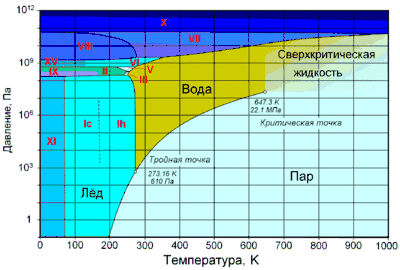
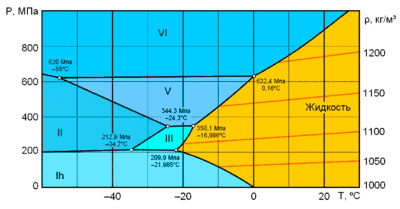
Элементы фазовой диаграммы
Тройные точки
| № | Фазы | Давление | Температура | Примечание | |||
|---|---|---|---|---|---|---|---|
| МПа | °C | K | |||||
| 1 | Пар | Вода | Лёд Ih | 611,657 Па | 0,01 | 273,16 | |
| 2 | Пар | Лёд Ih | Лёд XI | 0 | −201,0 | 72,15 | |
| 3 | Вода | Лёд Ih | Лёд III | 209,9 | −21,985 | 251,165 | |
| 4 | Лёд Ih | Лёд II | Лёд III | 212,9 | −34,7 | 238,45 | [5][6][7] |
| 5 | Лёд II | Лёд III | Лёд V | 344,3 | −24,3 | 248,85 | [5][6] |
| 6 | Лёд II | Лёд VI | Лёд XV | ~ 800 | −143 | 130 | Для D2O[8] |
| 7 | Вода | Лёд III | Лёд V | 350,1 | −16,986 | 256,164 | [5][6] |
| 8 | Вода | Лёд IV | Лёд XII | ~ 500—600 | ~ −6 | ~ 267 | |
| 9 | Лёд II | Лёд V | Лёд VI | ~ 620 | ~ −55 | ~ 218 | [10] |
| 10 | Вода | Лёд V | Лёд VI | 632,4 | 0.16 | 273,32 | [5][6] |
| 11 | Лёд VI | Лёд VIII | Лёд XV | ~ 1500 | −143 | 130 | Для D2O[8] |
| 12 | Лёд VI | Лёд VII | Лёд VIII | 2100 | ~ 5 | ~ 278 | [11][12] |
| 13 | Вода | Лёд VI | Лёд VII | 2216 | 81,85 | 355 | [5][6] |
| 14 | Лёд VII | Лёд VIII | Лёд X | 62 000 | −173 | 100 | [13] |
| 15 | Вода | Лёд VII | Лёд X | 47 000 | ~ 727 | ~ 1000 | [14][15] |
Кривая сублимации льда
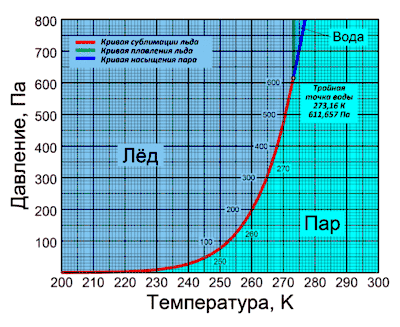
Кривая сублимации льда начинается в точке (0 Па; 0 K) и заканчивается в тройной точке воды (611,657 Па; 273,16 K). На этом участке при снижении температуры давление сублимации падает экспоненциально и при уже температуре 130 K составляет незначительную величину (10−8 Па).
С хорошей точностью давление сублимации на этом участке описывается экспонентой
где
Ошибка этой формулы — не более 1 % в диапазоне температур 240—273,16 K и не более 2,5 % диапазоне температур 140—240 K.
Более точно кривая сублимации описывается формулой, рекомендованной IAPWS (англ. International Association for the Properties of Water and Steam — Международная ассоциация по изучению свойств воды и пара)[16]:
где
Кривая плавления льда Ih
Кривая плавления льда Ih (то есть обычного льда) на фазовой диаграмме в области низких давлений представляет собой практически вертикальную прямую. Так, при переходе от тройной точки (611 Па) к атмосферному давлению (101 кПа) температура плавления падает всего на 0,008 K (с 273,16 до 273,15 K). Давление, необходимое для снижения температуры плавления на 1 K составляет около 132 атм. Кривая плавления по горизонтальной оси занимает диапазон температур 251,165—273,16 K (–21,985 ... 0,01 °C). Минимальная температура плавления (–21,985 °С) достигается при давлении 208,566 МПа (2058 атм).
Кривая плавления льда Ih — единственный фазовый переход, связанный с изменением агрегатного состояния воды, который имеет обратный наклон (при увеличении давления температура плавления уменьшается). Это обстоятельство (в соответствии с принципом ле Шателье) объясняется тем, что лёд Ih имеет меньшую плотность по сравнению с водой при том же давлении. Все остальные модификации льда тяжелее воды, их температура плавления при повышении давления увеличивается.
Кривая плавления описывается формулой, рекомендованной IAPWS[16]:
где
Кривая плавления льда III
Кривая плавления льда III начинается в точке минимальной температуры затвердевания воды (251,165 K; 208,566 МПа), где обычный лёд превращается в структурную модификацию III, и заканчивается в точке (256,164 K; 350,1 МПа), где проходит граница фаз III и V.
Кривая плавления описывается формулой, рекомендованной IAPWS[16]:
где
Кривая плавления льда V
Кривая плавления льда V начинается в точке (256,164 K; 350,1 МПа), на границе фаз III и V, и заканчивается в точке (273,31 K; 632,4 МПа), где проходит граница фаз V и VI.
Кривая плавления описывается формулой, рекомендованной IAPWS[16]:
где
Кривая плавления льда VI
Кривая плавления льда VI начинается в точке (273,31 K; 632,4 МПа), на границе фаз V и VI, и заканчивается в точке (355 K; 2216 МПа), где проходит граница фаз VI и VII.
Кривая плавления описывается формулой, рекомендованной IAPWS[16]:
где
Кривая плавления льда VII
Кривая плавления льда VII начинается в точке (355 K; 2216 МПа), на границе фаз VI и VII, и заканчивается в точке (715 K; 20,6 ГПа), где проходит граница фазы VII.
Кривая плавления описывается формулой, рекомендованной IAPWS[16]:
где
Кривая насыщения водяного пара
Кривая насыщения водяного пара начинается в тройной точке воды (273,16 K; 611,657 Па) и заканчивается в критической точке (647,096 К; 22,064 МПа). Она показывает температуру кипения воды при указанном давлении или, что то же самое, давление насыщенного водяного пара при указанной температуре. В критической точке плотность водяного пара достигает плотности воды и, таким образом, различие между этими агрегатными состояниями исчезает.
Согласно рекомендациям IAPWS, линия насыщения представляется в виде неявного квадратного уравнения относительно нормированной температуры θ и нормированного давления β[17]:
где
Для заданного абсолютного значения температуры T вычисляется нормированное значение θ и коэффициенты квадратного уравнения
после чего находится значение β
и абсолютное значение давления
Давление насыщенного водяного пара (кПа) при различных температурах
| T °C | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,6112 | 0,6571 | 0,7060 | 0,7581 | 0,8135 | 0,8726 | 0,9354 | 1,002 | 1,073 | 1,148 |
| 10 | 1,228 | 1,313 | 1,403 | 1,498 | 1,599 | 1,706 | 1,819 | 1,938 | 2,065 | 2,198 |
| 20 | 2,339 | 2,488 | 2,645 | 2,811 | 2,986 | 3,170 | 3,364 | 3,568 | 3,783 | 4,009 |
| 30 | 4,247 | 4,497 | 4,759 | 5,035 | 5,325 | 5,629 | 5,947 | 6,282 | 6,632 | 7,000 |
| 40 | 7,384 | 7,787 | 8,209 | 8,650 | 9,112 | 9,594 | 10,10 | 10,63 | 11,18 | 11,75 |
| 50 | 12,35 | 12,98 | 13,63 | 14,31 | 15,02 | 15,76 | 16,53 | 17,33 | 18,17 | 19,04 |
| 60 | 19,95 | 20,89 | 21,87 | 22,88 | 23,94 | 25,04 | 26,18 | 27,37 | 28,60 | 29,88 |
| 70 | 31,20 | 32,57 | 34,00 | 35,48 | 37,01 | 38,60 | 40,24 | 41,94 | 43,70 | 45,53 |
| 80 | 47,41 | 49,37 | 51,39 | 53,48 | 55,64 | 57,87 | 60,17 | 62,56 | 65,02 | 67,56 |
| 90 | 70,18 | 72,89 | 75,68 | 78,57 | 81,54 | 84,61 | 87,77 | 91,03 | 94,39 | 97,85 |
| 100 | 101,4 |
Ссылки
- IAPWS. Сайт Международной ассоциации по изучению свойств воды.
- Water Phase Diagram.
- Теплофизические свойства воды и водяного пара.
- Phase-boundary curves of water.
- Saturation vapor pressure formulations.
- Water (Data Page) (недоступная ссылка).
Примечания
- L. A.Guildner, D. P. Johnson, and F. E. Jones. Vapor pressure of water at its triple point (англ.) // J. Res. Nat. Bur. Stand.. — 1976. — Vol. 80A. — P. 505—521.
- M. J. Francis, N. Gulati and R. M. Pashley. The dispersion of natural oils in de-gassed water (англ.) // J. Colloid Interface Sci.. — 2006. — Vol. 299. — P. 673—677. (недоступная ссылка)
- R. M. Pashley, M. Rzechowicz, L. R. Pashley and M. J. Francis. De-gassed water Is a better cleaning agent (англ.) // J. Phys. Chem.. — 2005. — Vol. 109. — P. 1231—1238.
- R. M. Pashley, M. J. Francis and M. Rzechowicz. The hydrophobicity of non-aqueous liquids and their dispersion in water under de-gassed conditions (англ.) // Curr. Opin. Colloid Interface Sci.. — 2008. — Vol. 13. — P. 236—244. (недоступная ссылка)
- Release on the pressure along the melting and the sublimation curves of ordinary water substance. IAPWS, 1993.
- P. W. Bridgman Water, in the liquid and five solid forms, under pressure. Proc. Am. Acad. Arts Sci. 47, 1912, 439—558.
- J. L. F. Abascal, E. Sanz, R. G. Fernández, and C. Vega A potential model for the study of ices and amorphous water: TIP4P/Ice. J. Chem. Phys. 122 (2005) 234511.
- C. G. Salzmann, P. G. Radaelli, E. Mayer and J. L. Finney Ice XV: a new thermodynamically stable phase of ice. arXiv:0906.2489v1, cond-mat.mtrl-sci (2009).
- E. A. Zheligovskaya, G. G. Malenkov Crystalline water ices. Russian Chem. Rev. 75 (2006) 57-76.
- L. Mercury, P. Vieillard and Y. Tardy Thermodynamics of ice polymorphs and `ice-like' water in hydrates and hydroxides (недоступная ссылка). Appl. Geochem. 16 (2001) 161—181.
- D. Eisenberg and W. Kauzmann The structure and properties of water. Oxford University Press, London, 1969.
- L. Pauling The structure of water. В кн.: Hydrogen bonding, Ed. D. Hadzi and H. W. Thompson, Pergamon Press Ltd, London, 1959, pp 1-6.
- M. Song, H. Yamawaki, H. Fujihisa, M. Sakashita and K. Aoki Infrared investigation on ice VIII and the phase diagram of dense ices. Phys. Rev. B 68 (2003) 014106.
- B. Schwager, L. Chudinovskikh, A. Gavriliuk and R. Boehler Melting curve of H2O to 90 GPa measured in a laser-heated diamond cell. J. Phys: Condens. Matter 16 (2004) S1177-S1179.]
- A. F. Goncharov, N. Goldman, L. E. Fried, J. C. Crowhurst, I-F. W. Kuo, C. J. Mundy and J. M. Zaug Dynamic ionization of water under extreme conditions Архивная копия от 31 июля 2013 на Wayback Machine. Phys. Rev. Lett. 94 (2005)125508.
- Revised Release on the Pressure along the Melting and Sublimation Curves of Ordinary Water Substance. The International Association for the Properties of Water and Steam. Berlin, Germany, September 2008.
- Уравнения линии насыщения: А. А. Александров, К. А. Орлов, В. Ф. Очков Теплофизические свойства рабочих веществ теплоэнергетики: Интернет-справочник. — М.: Издательский дом МЭИ. 2009.
Литература
- J. L. Aragones, M. M. Conde, E. G. Noya, C. Vega. The phase diagram of water at high pressures as obtained by computer simulations of the TIP4P/2005 model: the appearance of a plastic crystal phase (англ.) // Physical Chemistry Chemical Physics : журнал. — 2009. — No. 11. — P. 543–555. — doi:10.1039/B812834K.
- C. Vega, J. L. F. Abascal, M. M. Conde and J. L. Aragones. What ice can teach us about water interactions: a critical comparison of the performance of different water models (англ.) // Faraday Discussions. — 2009. — Vol. 141. — P. 251—276. — arXiv:0901.1803v1.
- C. G. Salzmann, I. Kohl, T. Loerting, E. Mayer and A. Hallbrucker. Pure ices IV and XII from high-density amorphous ice (англ.) // Can. J. Phys.. — 2003. — Vol. 81. — P. 25—32. — doi:10.1139/P02-071.
- Александров А.А., Орлов К.А., Очков В.Ф. Теплофизические свойства рабочих веществ теплоэнергетики. — 2-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2017. — 226 с. с. — ISBN 978-5-383-01073-0.
- Jana Kalovaa and Radim Maresb. Equations for the Thermodynamic Properties at the Saturation Line in the Supercooled Water Region (англ.) // ICPWS XV : Preprint. — Berlin, September 8-11, 2008. — P. 1–5.
- W. Wagner, A. Saul, A. Pruβ. International Equations for the Pressure along the Melting and along the Sublimation Curve of Ordinary Water Substance (англ.) // J. Phys. Chem. Ref. Data : Preprint. — 1994. — Vol. 23, no. 3. — P. 515—527.
- Percy W . Bridgman. General survey of certain results in the field of high-pressure physics (англ.) : Nobel Lecture. — December 11, 1946. (недоступная ссылка)
- Д. В. Анцышкин, А. Н. Дунаева, О. Л. Кусков. Термодинамика фазовых переходов в системе лед-VI — лед-VII — вода (англ.) // Геохимия. — 2010. — No. 7. — P. 675—684. (недоступная ссылка)
- José Teixeira. The «puzzle» of Water Behavior at Low Temperature (англ.) // Water. — 2010. — No. 2. — P. 702—710.
- Wely Brasil Floriano, Marco Antonio Chaer Nascimento. Dielectric Constant and Density of Water as a Function of Pressure at Constant Temperature (англ.) // Brazilian Journal of Physics. — March, 2004. — Vol. 34, no. 1. — P. 38—41.