Тестовые функции для оптимизации

В прикладной математике, тестовые функции, известные как искусственные ландшафты, являются полезными для оценки характеристик алгоритмов оптимизации, таких как:

Скорость сходимости.
Точность.
Робастность.
Общая производительность.

В статье представлены некоторые тестовые функции с целью дать представление о различных ситуациях, с которыми приходится сталкиваться при преодолении подобных проблем.

В статье представлены общая формула уравнения, участок целевой функции, границы переменных и координаты глобального минимума.

Тестовые функции для одной цели оптимизации

Название	Формула	Глобальный минимум	Метод поиска
Функция Растригина	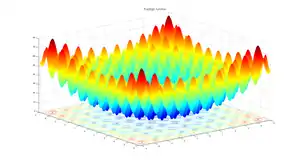$f(\mathbf {x} )=An+\sum _{i=1}^{n}\left[x_{i}^{2}-A\cos(2\pi x_{i})\right]$ ${\text{where: }}A=10$	$f(0,\dots ,0)=0$	$-5.12\leq x_{i}\leq 5.12$
Функция Экли	$f(x,y)=-20\exp \left[-0.2{\sqrt {0.5\left(x^{2}+y^{2}\right)}}\right]$ $-\exp \left[0.5\left(\cos 2\pi x+\cos 2\pi y\right)\right]+e+20$	$f(0,0)=0$	$-5\leq x,y\leq 5$
Функция сферы	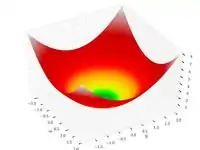$f({\boldsymbol {x}})=\sum _{i=1}^{n}x_{i}^{2}$	$f(x_{1},\dots ,x_{n})=f(0,\dots ,0)=0$	$-\infty \leq x_{i}\leq \infty$ , $1\leq i\leq n$
Функция Розенброка	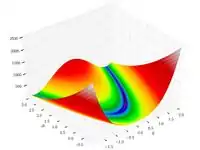$f({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(x_{i}-1\right)^{2}\right]$	${\text{Min}}={\begin{cases}n=2&\rightarrow \quad f(1,1)=0,\\n=3&\rightarrow \quad f(1,1,1)=0,\\n>3&\rightarrow \quad f(\underbrace {1,\dots ,1} _{n{\text{ times}}})=0\\\end{cases}}$	$-\infty \leq x_{i}\leq \infty$ , $1\leq i\leq n$
Функция Била	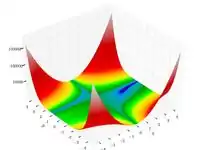$f(x,y)=\left(1.5-x+xy\right)^{2}+\left(2.25-x+xy^{2}\right)^{2}$ $+\left(2.625-x+xy^{3}\right)^{2}$	$f(3,0.5)=0$	$-4.5\leq x,y\leq 4.5$
Функция Гольдшейна-Прайса	$f(x,y)=\left[1+\left(x+y+1\right)^{2}\left(19-14x+3x^{2}-14y+6xy+3y^{2}\right)\right]$ $\left[30+\left(2x-3y\right)^{2}\left(18-32x+12x^{2}+48y-36xy+27y^{2}\right)\right]$	$f(0,-1)=3$	$-2\leq x,y\leq 2$
Функция Бута	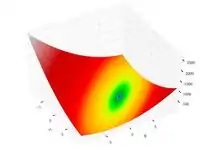$f(x,y)=\left(x+2y-7\right)^{2}+\left(2x+y-5\right)^{2}$	$f(1,3)=0$	$-10\leq x,y\leq 10$
Функция Букина N 6	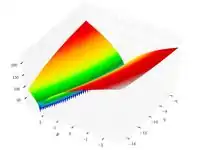$f(x,y)=100{\sqrt {\left\|y-0.01x^{2}\right\|}}+0.01\left\|x+10\right\|.\quad$	$f(-10,1)=0$	$-15\leq x\leq -5$ , $-3\leq y\leq 3$
Функция Матьяса	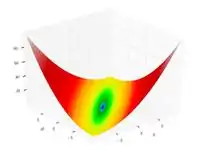$f(x,y)=0.26\left(x^{2}+y^{2}\right)-0.48xy$	$f(0,0)=0$	$-10\leq x,y\leq 10$
Функция Леви N 13	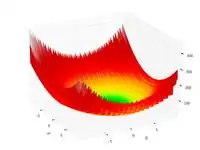$f(x,y)=\sin ^{2}3\pi x+\left(x-1\right)^{2}\left(1+\sin ^{2}3\pi y\right)$ $+\left(y-1\right)^{2}\left(1+\sin ^{2}2\pi y\right)$	$f(1,1)=0$	$-10\leq x,y\leq 10$
Функция Химмельблау	$f(x,y)=(x^{2}+y-11)^{2}+(x+y^{2}-7)^{2}.\quad$	${\text{Min}}={\begin{cases}f\left(3.0,2.0\right)&=0.0\\f\left(-2.805118,3.131312\right)&=0.0\\f\left(-3.779310,-3.283186\right)&=0.0\\f\left(3.584428,-1.848126\right)&=0.0\\\end{cases}}$	$-5\leq x,y\leq 5$
Функция трехгорбого верблюда	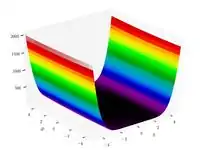$f(x,y)=2x^{2}-1.05x^{4}+{\frac {x^{6}}{6}}+xy+y^{2}$	$f(0,0)=0$	$-5\leq x,y\leq 5$
Функция Изома	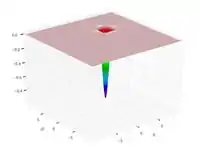$f(x,y)=-\cos \left(x\right)\cos \left(y\right)\exp \left(-\left(\left(x-\pi \right)^{2}+\left(y-\pi \right)^{2}\right)\right)$	$f(\pi ,\pi )=-1$	$-100\leq x,y\leq 100$
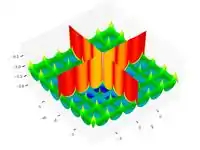Функция "крест на подносе" (Cross-in-tray function)	$f(x,y)=-0.0001\left[\left\|\sin x\sin y\exp \left(\left\|100-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right\|\right)\right\|+1\right]^{0.1}$	${\text{Min}}={\begin{cases}f\left(1.34941,-1.34941\right)&=-2.06261\\f\left(1.34941,1.34941\right)&=-2.06261\\f\left(-1.34941,1.34941\right)&=-2.06261\\f\left(-1.34941,-1.34941\right)&=-2.06261\\\end{cases}}$	$-10\leq x,y\leq 10$
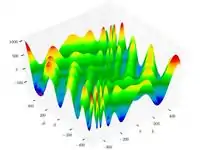Функция "подставка для яиц" (Eggholder function)	$f(x,y)=-\left(y+47\right)\sin {\sqrt {\left\|{\frac {x}{2}}+\left(y+47\right)\right\|}}-x\sin {\sqrt {\left\|x-\left(y+47\right)\right\|}}$	$f(512,404.2319)=-959.6407$	$-512\leq x,y\leq 512$
Табличная функция Хольдера	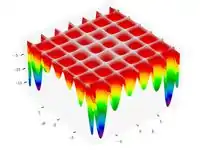$f(x,y)=-\left\|\sin x\cos y\exp \left(\left\|1-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right\|\right)\right\|$	${\text{Min}}={\begin{cases}f\left(8.05502,9.66459\right)&=-19.2085\\f\left(-8.05502,9.66459\right)&=-19.2085\\f\left(8.05502,-9.66459\right)&=-19.2085\\f\left(-8.05502,-9.66459\right)&=-19.2085\end{cases}}$	$-10\leq x,y\leq 10$
Функция МакКормика	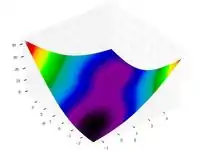$f(x,y)=\sin \left(x+y\right)+\left(x-y\right)^{2}-1.5x+2.5y+1$	$f(-0.54719,-1.54719)=-1.9133$	$-1.5\leq x\leq 4$ , $-3\leq y\leq 4$
Функция Шаффера N2	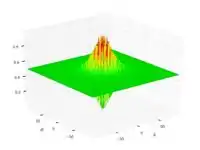$f(x,y)=0.5+{\frac {\sin ^{2}\left(x^{2}-y^{2}\right)-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}$	$f(0,0)=0$	$-100\leq x,y\leq 100$
Функция Шаффера N4	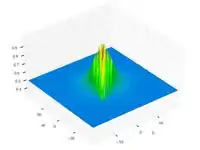$f(x,y)=0.5+{\frac {\cos ^{2}\left[\sin \left(\left\|x^{2}-y^{2}\right\|\right)\right]-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}$	$f(0,1.25313)=0.292579$	$-100\leq x,y\leq 100$
Функция Стыбинского-Танга	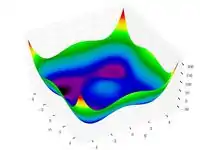$f({\boldsymbol {x}})={\frac {\sum _{i=1}^{n}x_{i}^{4}-16x_{i}^{2}+5x_{i}}{2}}$	$-39.16617n<f(\underbrace {-2.903534,\ldots ,-2.903534} _{n{\text{ times}}})<-39.16616n$	$-5\leq x_{i}\leq 5$ , $1\leq i\leq n$ ..

Тестовые функции для условной оптимизации

Название	Формула	Глобальный минимум	Метод поиска
функция розенброка, ограничена кубической и прямой[1]	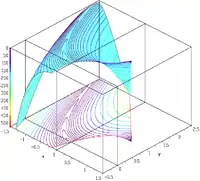$f(x,y)=(1-x)^{2}+100(y-x^{2})^{2}$ , subjected to: $(x-1)^{3}-y+1<0{\text{ and }}x+y-2<0$	$f(1.0,1.0)=0$	$-1.5\leq x\leq 1.5$ , $-0.5\leq y\leq 2.5$
Функция Розенброка, ограниченная диском[2]	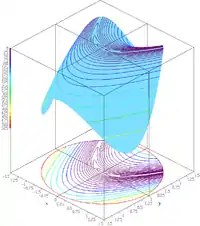$f(x,y)=(1-x)^{2}+100(y-x^{2})^{2}$ , subjected to: $x^{2}+y^{2}<2$	$f(1.0,1.0)=0$	$-1.5\leq x\leq 1.5$ , $-1.5\leq y\leq 1.5$
Ограниченная функция Мишры-Бёрда[3][4]	$f(x,y)=\sin(y)e^{\left[(1-\cos x)^{2}\right]}+\cos(x)e^{\left[(1-\sin y)^{2}\right]}+(x-y)^{2}$ , subjected to: $(x+5)^{2}+(y+5)^{2}<25$	$f(-3.1302468,-1.5821422)=-106.7645367$	$-10\leq x\leq 0$ , $-6.5\leq y\leq 0$
Модифицированная функция Таусенда[5]	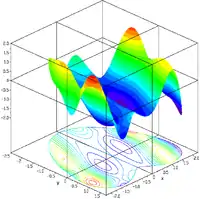$f(x,y)=-[\cos((x-0.1)y)]^{2}-x\sin(3x+y)$ , subjected to: $x^{2}+y^{2}<\left[2\cos t-{\frac {1}{2}}\cos 2t-{\frac {1}{4}}\cos 3t-{\frac {1}{8}}\cos 4t\right]^{2}+[2\sin t]^{2}$ where: t = Atan2(x,y)	$f(2.0052938,1.1944509)=-2.0239884$	$-2.25\leq x\leq 2.5$ , $-2.5\leq y\leq 1.75$
Функция Симонескуn[6]	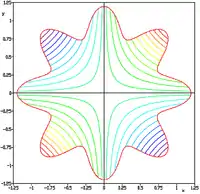$f(x,y)=0.1xy$ , subjected to: $x^{2}+y^{2}\leq \left[r_{T}+r_{S}\cos \left(n\arctan {\frac {x}{y}}\right)\right]^{2}$ ${\text{where: }}r_{T}=1,r_{S}=0.2{\text{ and }}n=8$	$f(\pm 0.85586214,\mp 0.85586214)=-0.072625$	$-1.25\leq x,y\leq 1.25$

Тестовые функции для многокритериальной оптимизации

Название / Рисунок	Формула	Минимум	Область поиска
Функция Бина и Корна	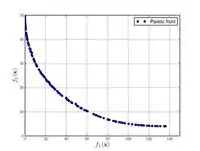${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=4x^{2}+4y^{2}\\f_{2}\left(x,y\right)&=\left(x-5\right)^{2}+\left(y-5\right)^{2}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)&=\left(x-5\right)^{2}+y^{2}\leq 25\\g_{2}\left(x,y\right)&=\left(x-8\right)^{2}+\left(y+3\right)^{2}\geq 7.7\\\end{cases}}$	$0\leq x\leq 5$ , $0\leq y\leq 3$
Chakong and Haimes function	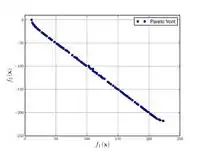${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=2+\left(x-2\right)^{2}+\left(y-1\right)^{2}\\f_{2}\left(x,y\right)&=9x-\left(y-1\right)^{2}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)&=x^{2}+y^{2}\leq 225\\g_{2}\left(x,y\right)&=x-3y+10\leq 0\\\end{cases}}$	$-20\leq x,y\leq 20$
Функция Ффонсеки и Флеминга	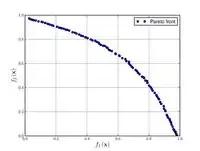${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=1-\exp \left(-\sum _{i=1}^{n}\left(x_{i}-{\frac {1}{\sqrt {n}}}\right)^{2}\right)\\f_{2}\left({\boldsymbol {x}}\right)&=1-\exp \left(-\sum _{i=1}^{n}\left(x_{i}+{\frac {1}{\sqrt {n}}}\right)^{2}\right)\\\end{cases}}$		$-4\leq x_{i}\leq 4$ , $1\leq i\leq n$
Test function 4	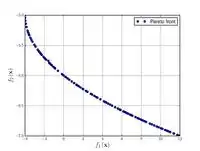${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=x^{2}-y\\f_{2}\left(x,y\right)&=-0.5x-y-1\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)&=6.5-{\frac {x}{6}}-y\geq 0\\g_{2}\left(x,y\right)&=7.5-0.5x-y\geq 0\\g_{3}\left(x,y\right)&=30-5x-y\geq 0\\\end{cases}}$	$-7\leq x,y\leq 4$
Функция Курсаве	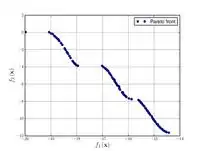${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{2}\left[-10\exp \left(-0.2{\sqrt {x_{i}^{2}+x_{i+1}^{2}}}\right)\right]\\&\\f_{2}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{3}\left[\left\|x_{i}\right\|^{0.8}+5\sin \left(x_{i}^{3}\right)\right]\\\end{cases}}$		$-5\leq x_{i}\leq 5$ , $1\leq i\leq 3$ .
Schaffer function N. 1	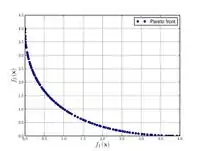${\text{Minimize}}={\begin{cases}f_{1}\left(x\right)&=x^{2}\\f_{2}\left(x\right)&=\left(x-2\right)^{2}\\\end{cases}}$		$-A\leq x\leq A$ . Values of $A$ form $10$ to $10^{5}$ have been used successfully. Higher values of $A$ increase the difficulty of the problem.
Schaffer function N. 2	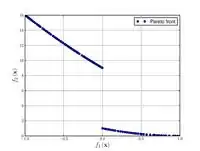${\text{Minimize}}={\begin{cases}f_{1}\left(x\right)&={\begin{cases}-x,&{\text{if }}x\leq 1\\x-2,&{\text{if }}1<x\leq 3\\4-x,&{\text{if }}3<x\leq 4\\x-4,&{\text{if }}x>4\\\end{cases}}\\f_{2}\left(x\right)&=\left(x-5\right)^{2}\\\end{cases}}$		$-5\leq x\leq 10$ .
Объективная функция Полони2	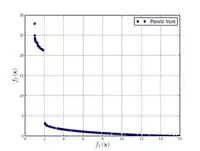${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=\left[1+\left(A_{1}-B_{1}\left(x,y\right)\right)^{2}+\left(A_{2}-B_{2}\left(x,y\right)\right)^{2}\right]\\f_{2}\left(x,y\right)&=\left(x+3\right)^{2}+\left(y+1\right)^{2}\\\end{cases}}$ ${\text{where}}={\begin{cases}A_{1}&=0.5\sin \left(1\right)-2\cos \left(1\right)+\sin \left(2\right)-1.5\cos \left(2\right)\\A_{2}&=1.5\sin \left(1\right)-\cos \left(1\right)+2\sin \left(2\right)-0.5\cos \left(2\right)\\B_{1}\left(x,y\right)&=0.5\sin \left(x\right)-2\cos \left(x\right)+\sin \left(y\right)-1.5\cos \left(y\right)\\B_{2}\left(x,y\right)&=1.5\sin \left(x\right)-\cos \left(x\right)+2\sin \left(y\right)-0.5\cos \left(y\right)\end{cases}}$		$-\pi \leq x,y\leq \pi$
Функция Зистера-Дьеба-Тери N. 1	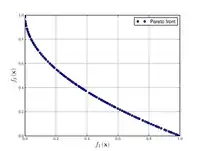${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}\\\end{cases}}$		$0\leq x_{i}\leq 1$ , $1\leq i\leq 30$ .
Функция Зистера-Дьеба-Тери N. 2	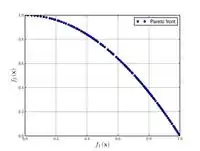${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}$		$0\leq x_{i}\leq 1$ , $1\leq i\leq 30$ .
Функция Зистера-Дьеба-Териn N. 3	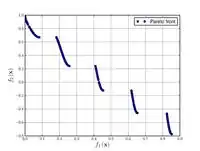${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)\sin \left(10\pi f_{1}\left({\boldsymbol {x}}\right)\right)\end{cases}}$		$0\leq x_{i}\leq 1$ , $1\leq i\leq 30$ .
Функция Зистера-Дьеба-ТериN. 4	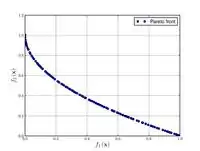${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=91+\sum _{i=2}^{10}\left(x_{i}^{2}-10\cos \left(4\pi x_{i}\right)\right)\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}\end{cases}}$		$0\leq x_{1}\leq 1$ , $-5\leq x_{i}\leq 5$ , $2\leq i\leq 10$
Функция Зистера-Дьеба-Тери N. 6	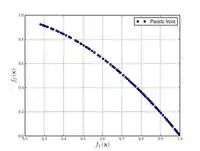${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=1-\exp \left(-4x_{1}\right)\sin ^{6}\left(6\pi x_{1}\right)\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=1+9\left[{\frac {\sum _{i=2}^{10}x_{i}}{9}}\right]^{0.25}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}$		$0\leq x_{i}\leq 1$ , $1\leq i\leq 10$ .
Функция Виннета	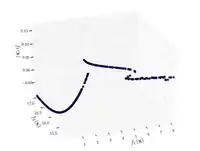${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=0.5\left(x^{2}+y^{2}\right)+\sin \left(x^{2}+y^{2}\right)\\f_{2}\left(x,y\right)&={\frac {\left(3x-2y+4\right)^{2}}{8}}+{\frac {\left(x-y+1\right)^{2}}{27}}+15\\f_{3}\left(x,y\right)&={\frac {1}{x^{2}+y^{2}+1}}-1.1\exp \left(-\left(x^{2}+y^{2}\right)\right)\\\end{cases}}$		$-3\leq x,y\leq 3$ .
Функция Осызки и Кунду	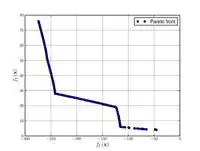$F_{1}(x)=-25\left(x_{1}-2\right)^{2}-\left(x_{2}-2\right)^{2}$ $-\left(x_{3}-1\right)^{2}-\left(x_{4}-4\right)^{2}-\left(x_{5}-1\right)^{2}$ ${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=F_{1}(x)\\f_{2}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{6}x_{i}^{2}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left({\boldsymbol {x}}\right)&=x_{1}+x_{2}-2\geq 0\\g_{2}\left({\boldsymbol {x}}\right)&=6-x_{1}-x_{2}\geq 0\\g_{3}\left({\boldsymbol {x}}\right)&=2-x_{2}+x_{1}\geq 0\\g_{4}\left({\boldsymbol {x}}\right)&=2-x_{1}+3x_{2}\geq 0\\g_{5}\left({\boldsymbol {x}}\right)&=4-\left(x_{3}-3\right)^{2}-x_{4}\geq 0\\g_{6}\left({\boldsymbol {x}}\right)&=\left(x_{5}-3\right)^{2}+x_{6}-4\geq 0\end{cases}}$	$0\leq x_{1},x_{2},x_{6}\leq 10$ , $1\leq x_{3},x_{5}\leq 5$ , $0\leq x_{4}\leq 6$ .
CTP1 function (2 variables)	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=x\\f_{2}\left(x,y\right)&=\left(1+y\right)\exp \left(-{\frac {x}{1+y}}\right)\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)&={\frac {f_{2}\left(x,y\right)}{0.858\exp \left(-0.541f_{1}\left(x,y\right)\right)}}\geq 1\\g_{1}\left(x,y\right)&={\frac {f_{2}\left(x,y\right)}{0.728\exp \left(-0.295f_{1}\left(x,y\right)\right)}}\geq 1\end{cases}}$	$0\leq x,y\leq 1$ .
Проблема Констр-Экса	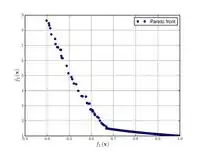${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=x\\f_{2}\left(x,y\right)&={\frac {1+y}{x}}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)&=y+9x\geq 6\\g_{1}\left(x,y\right)&=-y+9x\geq 1\\\end{cases}}$	$0.1\leq x\leq 1$ , $0\leq y\leq 5$

См. также

Литература

Пантелеев А. В., Метлицкая Д. В., Е.А. Алешина Методы глобальной оптимизации. Метаэвристические стратегии и алгоритмы // М.: Вузовская книга. 2013. 244 с. ISBN 978-5-9502-0743-3
Сергиенко А. С. Тестовые функции для глобальной оптимизации.

Ссылки

Тестирование алгоритмов многомерной оптимизации

Примечания

Simionescu, P.A. (September 29 – October 2, 2002). «New Concepts in Graphic Visualization of Objective Functions» in ASME 2002 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.: 891–897. Дата обращения: 7 January 2017.
Solve a Constrained Nonlinear Problem - MATLAB & Simulink (неопр.). www.mathworks.com. Дата обращения: 29 августа 2017.
Bird Problem (Constrained) | Phoenix Integration (неопр.) (недоступная ссылка). wayback.archive.org. Дата обращения: 29 августа 2017. Архивировано 29 декабря 2016 года.
Mishra, Sudhanshu. Some new test functions for global optimization and performance of repulsive particle swarm method (англ.) // MPRA Paper : journal. — 2006.
Townsend, Alex Constrained optimization in Chebfun (неопр.). chebfun.org (январь 2014). Дата обращения: 29 августа 2017.
Simionescu, P.A. Computer Aided Graphing and Simulation Tools for AutoCAD Users (англ.). — 1st. — Boca Raton, FL: CRC Press, 2014. — ISBN 978-1-4822-5290-3.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Simionescu, P.A. (September 29 – October 2, 2002). «New Concepts in Graphic Visualization of Objective Functions» in ASME 2002 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.: 891–897. Дата обращения: 7 January 2017.

[2] Solve a Constrained Nonlinear Problem - MATLAB & Simulink (неопр.). www.mathworks.com. Дата обращения: 29 августа 2017.

[3] Bird Problem (Constrained) | Phoenix Integration (неопр.) (недоступная ссылка). wayback.archive.org. Дата обращения: 29 августа 2017. Архивировано 29 декабря 2016 года.

[4] Mishra, Sudhanshu. Some new test functions for global optimization and performance of repulsive particle swarm method (англ.) // MPRA Paper : journal. — 2006.

[5] Townsend, Alex Constrained optimization in Chebfun (неопр.). chebfun.org (январь 2014). Дата обращения: 29 августа 2017.

[6] Simionescu, P.A. Computer Aided Graphing and Simulation Tools for AutoCAD Users (англ.). — 1st. — Boca Raton, FL: CRC Press, 2014. — ISBN 978-1-4822-5290-3.