Функция Розенброка
Функция Розенброка (англ. Rosenbrock function, Rosenbrock's valley, Rosenbrock's banana function) — невыпуклая функция, используемая для оценки производительности алгоритмов оптимизации, предложенная Ховардом Розенброком в 1960 году[1]. Считается, что поиск глобального минимума для данной функции является нетривиальной задачей.
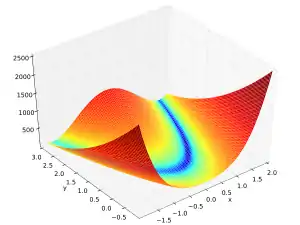
Является примером тестовой функции для локальных методов оптимизации. Имеет минимум 0 в точке (1,1)[2].
Каноническое определение
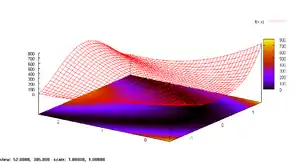
Функция Розенброка для двух переменных определяется как:
Она имеет глобальный минимум в точке где .
Многомерное обобщение
Встречаются два классических варианта многомерного обобщения функции Розенброка.
В первом случае, как сумма несвязанных двумерных функций Розенброка:
Более сложным вариантом является:
Существует также вероятностное обобщение функции Розенброка, предложенное англ. Xin-She Yang[5]:
где случайные переменные являются равномерно распределёнными Unif(0,1).
См. также
Примечания
- Rosenbrock, H.H. An automatic method for finding the greatest or least value of a function (англ.) // The Computer Journal : journal. — 1960. — Vol. 3. — P. 175—184. — ISSN 0010-4620. — doi:10.1093/comjnl/3.3.175.
- Жилинискас А., Шатлянис В. Поиск оптимума: компьютер расширяет возможности. - М.: Наука, 1989, с. 14, ISBN 5-02-006737-7
- L C W Dixon, D J Mills. Effect of Rounding errors on the Variable Metric Method. Journal of Optimization Theory and Applications 80, 1994.
- Generalized Rosenbrock's function (недоступная ссылка). Дата обращения: 16 сентября 2008. Архивировано 26 сентября 2008 года.
- Yang X.-S. and Deb S., Engineering optimization by cuckoo search, Int. J. Math. Modelling Num. Optimisation, Vol. 1, No. 4, 330—343 (2010).
Литература
- Методические указания к исследовательской лабораторной работе по дисциплине «Математические основы кибернетики» // Крушель Е. Г., Степанченко О. В. (недоступная ссылка с 13-05-2013 [3209 дней] — история)
- Rosenbrock, H. H. (1960), An automatic method for finding the greatest or least value of a function, The Computer Journal Т. 3: 175-184, MR: 0136042, ISSN 0010-4620, DOI 10.1093/comjnl/3.3.175
Ссылки
- Rosenbrock function plot in 3D (англ.).
- Minimizing the Rosenbrock Function by Michael Croucher, The Wolfram Demonstrations Project (англ.).
- Weisstein, Eric W. Rosenbrock Function (англ.) на сайте Wolfram MathWorld. (англ.)
- Solving non-linear models with Compact Quasi Newton solver part 1 (англ.).