Теорема Эрдёша — Секереша

Теорема Э́рдёша — Се́кереша в комбинаторике — утверждение, уточняющее одно из следствий теоремы Рамсея для финитного случая. В то время как теорема Рамсея облегчает доказательство того, что каждая последовательность разных действительных чисел содержит монотонно возрастающую бесконечную подпоследовательность или монотонно убывающую бесконечную подпоследовательность, результат, доказанный Палом Эрдёшем и Дьёрдем Секерешем, идёт дальше. Для данных r, s они показали, что любая последовательность разных чисел длины не менее (r-1)(s-1)+1 содержит монотонно возрастающую подпоследовательность длины r или монотонно убывающую длины s. Доказательство появилось в той же самой работе 1935 года, что и задача со счастливым концом.[1]

Цепь из четырёх рёбер с положительным наклоном на множестве из 17 точек. Если образовать последовательность y-координат этих точек, в порядке их x-координат, теорема Эрдёша — Секереша гарантирует, что существует либо цепь такого типа, либо цепь той же длины, в которой все наклоны отрицательны. Однако, если центральная точка отсутствует, такая цепь не существовала бы.

Пример

Для r=3 и s=2, формула говорит, что любая перестановка трёх чисел имеет возрастающую подпоследовательность длиной три или убывающую подпоследовательность длиной два. Из шести перестановок чисел 1,2,3:

  • 1,2,3 имеет возрастающую подпоследовательность длиной три
  • 1,3,2 имеет убывающую подпоследовательность 3,2
  • 2,1,3 имеет убывающую подпоследовательность 2,1
  • 2,3,1 имеет две убывающие подпоследовательности: 2,1 и 3,1
  • 3,1,2 имеет две убывающие подпоследовательности: 3,1 и 3,2
  • 3,2,1 имеет три убывающие подпоследовательности длины 2: 3,2, 3,1, и 2,1.

Геометрическая интерпретация

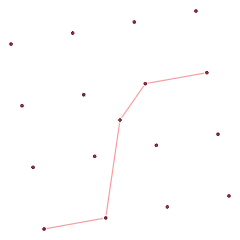
Позиции чисел в последовательности можно интерпретировать как x-координаты точек в евклидовой плоскости, а сами числа как y-координаты; с другой стороны, для любого множества точек на плоскости их y-координаты, упорядоченные по их x-координатам, образуют последовательность чисел (если только два числа не имеют двух одинаковых x-координат). При такой связи между последовательностями и множествами точек теорему Эрдёша — Секереша можно интерпретировать как утверждение, что для любого множества из rs + 1 или более точек найдётся ломаная из r положительно наклоненных отрезков или из s отрезков с отрицательным наклоном. Например, при r = s = 4 любое множество из 17 или более точек имеет цепь из четырёх рёбер, в котором все наклоны имеют одинаковый знак.

Доказательство

Теорема Эрдёша — Секереша может быть доказана несколькими разными способами; Майкл Стил дает обзор шести разных доказательств теоремы, в том числе с использованием принципа Дирихле и теоремы Дилуорса.[2] Прочие способы доказательства, приводимые Стилом, включают оригинальное доказательство Эрдёша и Секереша и доказательство Блэквелла, Ловаса и самого Стила.[3][4][5]Доказательство также есть в книге[6].

Принцип Дирихле
Основная статья: Принцип Дирихле

В последовательности длины (r − 1)(s − 1) + 1 пометим каждое число ni парой (ai,bi), где ai - длина наибольшей монотонно возрастающей подпоследовательности, заканчивающейся на ni, bi длина наибольшей монотонно убывающей подпоследовательности, заканчивающейся на ni. Все числа в последовательности помечены различными парами: если i < j и ni ≤ nj, то ai < aj; если ni ≥ nj, то bi < bj. Но есть всего (r − 1)(s − 1) возможных пар, если ai не больше r − 1, а bi не больше s − 1, так что по принципу Дирихле существует i, для которого ai или bi выходит за пределы этого ограничения. Если ai выходит за пределы, то ni - часть возрастающей подпоследовательности длины не меньше r, если bi выходит за пределы, то ni - часть убывающей подпоследовательности длины не меньше s.

Теорема Дилуорса
Основная статья: Теорема Дилуорса

См. также

Примечания
  1. Erdős, Paul; Szekeres, George (1935), A combinatorial problem in geometry, Compositio Mathematica Т. 2: 463–470, <http://www.numdam.org/item?id=CM_1935__2__463_0>
  2. Steele, J. Michael (1995), Variations on the monotone subsequence theme of Erdős and Szekeres, in Aldous, David; Diaconis, Persi & Spencer, Joel et al., Discrete Probability and Algorithms, vol. 72, IMA Volumes in Mathematics and its Applications, Springer-Verlag, с. 111–131, <http://www-stat.wharton.upenn.edu/~steele/Publications/PDF/VOTMSTOEAS.pdf>.
  3. Blackwell, Paul (1971), An alternative proof of a theorem of Erdős and Szekeres, American Mathematical Monthly Т. 78 (3): 273–273, DOI 10.2307/2317525.
  4. Hammersley, J. M. (1972), A few seedlings of research, Proc. 6th Berkeley Symp. Math. Stat. Prob., University of California Press, с. 345–394.
  5. Lovász, László (1979), Solution to Exercise 14.25, Combinatorial Problems and Exercises, North-Holland.
  6. Комбинаторная теория, 1982, с. 514.

Источники

Литература
  • Айгнер М. Комбинаторная теория. — М.: Мир, 1982. — 555 с.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.