Теорема Рауса

Теорема Рауса определяет отношение между площадями заданного треугольника и треугольника, образованного тремя попарно пересекающимися чевианами. Теорема утверждает, что если в треугольнике $ABC$ точки $D$ , $E$ и $F$ лежат на сторонах $BC$ , $CA$ и $AB$ соответственно, то, обозначив ${\tfrac {CD}{BD}}$ $=x$ , ${\tfrac {AE}{CE}}$ $=y$ и ${\tfrac {BF}{AF}}$ $=z$ , ориентированная площадь треугольника, образованного чевианами $AD$ , $BE$ и $CF$ по отношению к площади треугольника $ABC$ выражается соотношением

{\frac {(xyz-1)^{2}}{(xy+y+1)(yz+z+1)(zx+x+1)}}

Теорема была доказана Э. Дж. Раусом на 82 странице его Treatise on Analytical Statics with Numerous Examples в 1896 году. В частном случае, $x=y=z=2$ теорема представляет собой известную теорему об one-seventh area triangle. В случае $x=y=z=1$ медианы пересекаются в центроиде.

Доказательство

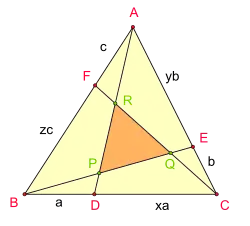
Положим площадь треугольника $ABC$ равной $1$ . Для треугольника $ABD$ и линии $FRC$ , используя теорему Менелая, получим:

{\frac {AF}{FB}}\times {\frac {BC}{CD}}\times {\frac {DR}{RA}}=1

Тогда ${\frac {DR}{RA}}={\frac {BF}{FA}}\times {\frac {DC}{CB}}={\frac {zx}{x+1}}$ Поэтому площадь треугольника $ARC$ равна

S_{ARC}={\frac {AR}{AD}}S_{ADC}={\frac {AR}{AD}}\times {\frac {DC}{BC}}S_{ABC}={\frac {x}{zx+x+1}}

Аналогично, получаем: $S_{BPA}={\frac {y}{xy+y+1}}$ и $S_{CQB}={\frac {z}{yz+z+1}}$ Таким образом, площадь треугольника $PQR$ равна:

\displaystyle S_{PQR}=S_{ABC}-S_{ARC}-S_{BPA}-S_{CQB}

=1-{\frac {x}{zx+x+1}}-{\frac {y}{xy+y+1}}-{\frac {z}{yz+z+1}}

={\frac {(xyz-1)^{2}}{(xz+x+1)(yx+y+1)(zy+z+1)}}.

Ссылки

Murray S. Klamkin, A. Liu (1981) «Three more proofs of Routh’s theorem», Crux Mathematicorum 7:199-203.
H. S. M. Coxeter (1969) Introduction to Geometry, pp. 211, 219-220, 2nd edition, Wiley, New York.
J. S. Kline, D. Velleman. (1995) «Yet another proof of Routh’s theorem» (1995) Crux Mathematicorum 21:37-40
Jay Warendorff. Routh’s Theorem The Wolfram Demonstrations Project.
Weisstein, Eric W. Routh's Theorem (англ.) на сайте Wolfram MathWorld.
Routh’s Theorem by Cross Products - MathPages
Ayoub, Ayoub B. (2011/2012) «Routh’s theorem revisited», Mathematical Spectrum 44 (1): 24-27.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.