Теорема Пуанкаре — Бендиксона
Теорема Пуанкаре — Бендиксона — теорема в теории динамических систем, описывающая возможные типы предельного поведения траектории векторного поля на плоскости или на сфере. Теорема утверждает, что предельное поведение траекторий в этом случае регулярно, и не может быть хаотическим (невозможно даже наличие всюду плотных орбит).
Формулировка теоремы
|
Пусть задано -гладкое векторное поле на сфере или на плоскости или в некоторой области плоскости (в последнем случае, направленное внутрь на границе области), имеющее лишь конечное число особых точек. Тогда ω-предельное множество любой траектории — это либо (1) особая точка, либо (2) периодическая траектория, либо (3) полицикл (объединение особых точек и соединяющих их отрезков траекторий). Аналогичное утверждение имеет место и для α-предельных множеств. |
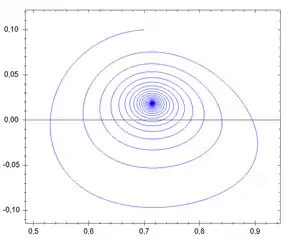
Пример случая 1. 
Пример случая 2. 
Пример случая 3.
Замечания
См. также
- Поток Черри
- Мешок Бендиксона
- Теорема Бендиксона об отсутствии замкнутых траекторий
Примечания
Литература
- Каток А. Б., Хассельблат Б. Введение в современную теорию динамических систем = Introduction to the Modern Theory of Dynamical Systems / пер. с англ. А. Кононенко при участии С. Ферлегера. — М.: Факториал, 1999. — С. 455. — 768 с. — ISBN 5-88688-042-9.
- Ю.С. Ильяшенко. Эволюционные процессы и философия общности положения, М.: МЦНМО, 2007.