Полицикл

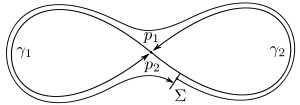
Полициклом векторного поля называется циклически занумерованный набор особых точек ${\displaystyle p_{1},\ldots ,p_{n}}$ (возможно, с повторениями) и набор дуг фазовых кривых ${\displaystyle \gamma _{1},\ldots ,\gamma _{n}}$ (без повторений), последовательно соединяющих указанные особые точки — то есть дуга ${\displaystyle \gamma _{j}}$ соединяет точки ${\displaystyle p_{j}}$ и ${\displaystyle p_{j+1}}$, где ${\displaystyle p_{n+1}\equiv p_{1}}$, ${\displaystyle j=1,\ldots ,n}$.

Говоря неформально, цикличность полицикла — это количество предельных циклов, «рождающихся из полицикла» в результате малого возмущения системы. Чтобы придать этому определению строгий смысл, необходимо указать, какие именно малые возмущения рассматриваются — иными словами, включить систему с полициклом в некоторое семейство. Точное определение звучит следующим образом:

Определение. Рассмотрим некоторое семейство векторных полей ${\displaystyle \{v_{\varepsilon }(x)\}}$, зависящее от (вообще говоря, многомерного) параметра ${\displaystyle \varepsilon \in \mathbb {R} ^{k}}$. Пусть при ${\displaystyle \varepsilon =\varepsilon _{*}}$ система имеет полицикл ${\displaystyle \gamma }$. Цикличностью полицикла ${\displaystyle \gamma }$ в семействе ${\displaystyle \{v_{\varepsilon }\}}$ называется такое минимальное число ${\displaystyle \mu }$, что найдётся такая окрестность полицикла ${\displaystyle U\supset \gamma }$ и такая окрестность ${\displaystyle V}$ критического значения параметра (${\displaystyle \mathbb {R} ^{k}\supset V\ni \varepsilon _{*}}$), что для всех ${\displaystyle \varepsilon \in V}$ в области ${\displaystyle U}$ одновременно существует не более ${\displaystyle \mu }$ предельных циклов, причём хаусдорфово расстояние между этими циклами и ${\displaystyle \gamma }$ стремится к нулю при ${\displaystyle \varepsilon \to \varepsilon _{*}}$.

• В. Ю. Калошин. Проблема Гильберта — Арнольда и оценка цикличности полициклов на плоскости и в пространстве. Функц. анализ и его прил., 35:2 (2001), 78–81.