Сфероид Маклорена

Угловая скорость для сфероида Маклорена

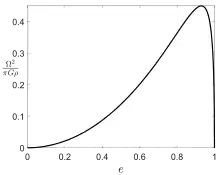
Для сплюснутого сфероида с большой полуосью ${\displaystyle a}$ и малой полуосью ${\displaystyle c}$ угловая скорость ${\displaystyle \Omega }$ задаётся формулой Маклорена

${\displaystyle {\frac {\Omega ^{2}}{\pi G\rho }}={\frac {2{\sqrt {1-e^{2}}}}{e^{3}}}(3-2e^{2})\sin ^{-1}e-{\frac {6}{e^{2}}}(1-e^{2}),\quad e^{2}=1-{\frac {c^{2}}{a^{2}}},}$

где ${\displaystyle e}$ является эксцентриситетом меридионального сечения сфероида, ${\displaystyle \rho }$ — плотность, ${\displaystyle G}$ — гравитационная постоянная, ${\displaystyle \sin ^{-1}e=\arcsin e}$. Формула предсказывает два возможных типа фигуры равновесия при ${\displaystyle \Omega \rightarrow 0}$, одной из них является сфера (${\displaystyle e\rightarrow 0}$), другой является плоский сфероид (${\displaystyle e\rightarrow 1}$). Максимальная угловая скорость возникает при эксцентриситете ${\displaystyle e=0,92995}$, значение скорости равно ${\displaystyle \Omega ^{2}/(\pi G\rho )=0,449331}$, то есть выше этой скорости фигуры равновесия не существует. Это противоречит данным. Причиной противоречия может быть наличие двух нереалистичных предположений: одно состоит в однородности распределения плотности, другое — в том, что форма поверхности представляет собой простую квадрику. Угловой момент ${\displaystyle L}$ задаётся выражением

${\displaystyle {\frac {L}{\sqrt {GM^{3}{\bar {a}}}}}={\frac {\sqrt {3}}{5}}\left({\frac {a}{\bar {a}}}\right)^{2}{\sqrt {\frac {\Omega ^{2}}{\pi G\rho }}}\ ,\quad {\bar {a}}=(a^{2}c)^{1/3},}$

где ${\displaystyle M}$ — масса сфероида, ${\displaystyle {\bar {a}}}$ — средний радиус, то есть радиус сферы такого же объёма, что и сфероид.

Для сфероида Маклорена с эксцентриситетом более 0,812670[3] эллипсоид Якоби с тем же угловым моментом обладает меньшей полной энергией. Если такой эллипсоид состоит из вязкой жидкости и не испытывает возмущений, способных нарушить симметрию вращения, то он вытянется и примет форму эллипсоида Якоби, при этом часть энергии перейдёт в тепловую форму. Для аналогичного сфероида из невязкой жидкости возмущения приведут к незатухающим колебаниям.

Сфероид Маклорена с эксцентриситетом более 0,952887[3] динамически неустойчив. Даже если объект состоит из невязкой жидкости и не теряет энергию, малые возмущения будут расти по экспоненциальному закону. Динамическая неустойчивость подразумевает вековую неустойчивость.[4]