Сферический сегмент
Сфери́ческий сегме́нт — поверхность, часть сферы, отсекаемая от неё некоторой плоскостью. Плоскость отсекает два сегмента: меньший сегмент называется также сферическим кругом[1]. Если секущая плоскость проходит через центр сферы, так что высота обоих сегментов равна радиусу сферы, то каждый из таких сферических сегментов называют полусферой.
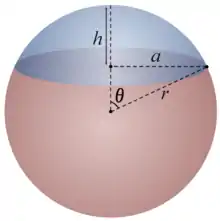
.
Шарово́й сегме́нт — геометрическое тело, ограниченное сферическим сегментом и совпадающим с ним границей кругом-основанием.
Объём и площадь поверхности
Если радиус основания сегмента равен , высота сегмента равна , тогда объём шарового сегмента равен [2]
- ,
площадь поверхности сегмента равна
или
- .
Параметры , и связаны соотношениями
- ,
- .
Подстановка последнего выражения в первую формулу для вычисления площади приводит к равенству
- .
Заметим, что в верхней части сферы (синий сегмент на рисунке) , в нижней части сферы , следовательно, для обоих сегментов справедливо выражение и можно привести другое выражение для объёма:
- .
Формула для определения объёма также может быть получена при интегрировании поверхности вращения:
- .
Применение
Объём объединения и пересечения двух пересекающихся сфер
Объём объединения двух сфер радиусов r1 и r2 равен [3]
- ,
где
является суммой объёмов двух сфер по отдельности, а
является суммой объёмов двух сферических сегментов, образующих пересечение данных сфер. Пусть d < r1 + r2 — расстояние между центрами сфер, тогда исключение величин h1 и h2 приводит к выражению [4][5]
- .
Площадь поверхности, ограниченной кругами разных широт
Площадь поверхности, ограниченной кругами разных широт, является разностью площадей поверхности двух соответствующих сферических сегментов. Для сферы радиуса r и широт φ1 и φ2 данная площадь равна [6]
- .
Площадь квадратного участка поверхности шара
- .
Например, площадь участка поверхности Земли со сторонами равными 1 градусу: A = 8 * (6 378 км) (1-cos(0,5))= 12391 км, 1 квадратная секунда поверхности Земли = 12391 км/ (60 * 60) = 956м
Обобщения
Сечения других тел
Сфероидальный сегмент получается при отсечении части сфероида таким образом, что она обладает круговой симметрией (обладает осью вращения). Аналогичным образом определяют эллипсоидальный сегмент.
Сегмент гиперсферы
Объём -мерного сегмента гиперсферы высотой и радиуса в -мерном евклидовом пространстве определяется по формуле [7]
где (гамма-функция) задается выражением .
Выражение для объёма можно переписать в терминах объёма единичного -мерного шара и гипергеометрической функции или регуляризованной неполной бета-функции как
- .
Формула для площади поверхности может быть записана в терминах площади поверхности единичного -мерного шара как
- ,
где .
Также справедливы следующие формулы[8]: , где ,
.
При
.
Было показано[9], что при и , где — стандартное нормальное распределение.
Литература
- А. И. Маркушевич, А. Я. Хинчин, П. С. Александров. Основные понятия сферической геометрии // Энциклопедия элементарной математики. Книга 4 - Геометрия. — Москва: ГИФМЛ, 1963.
Примечания
- Энциклопедия элементарной математики, 1963, с. 519-520.
- Polyanin, Andrei D & Manzhirov, Alexander V. (2006), Handbook of Mathematics for Engineers and Scientists, CRC Press, с. 69, ISBN 9781584885023, <https://books.google.com/books?id=ge6nk9W0BCcC&pg=PA69>.
- Connolly, Michael L. Computation of molecular volume (англ.) // J. Am. Chem. Soc : journal. — 1985. — Vol. 107. — P. 1118—1124. — doi:10.1021/ja00291a006.
- Pavani, R.; Ranghino, G. A method to compute the volume of a molecule (неопр.) // Comput. Chem.. — 1982. — Т. 6. — С. 133—135. — doi:10.1016/0097-8485(82)80006-5.
- Bondi, A. Van der Waals volumes and radii (англ.) // J. Phys. Chem. : journal. — 1964. — Vol. 68. — P. 441—451. — doi:10.1021/j100785a001.
- Scott E. Donaldson, Stanley G. Siegel. Successful Software Development. Дата обращения: 29 августа 2016.
- Li, S. Concise Formulas for the Area and Volume of a Hyperspherical Cap (англ.) // Asian J. Math. Stat. : journal. — 2011. — Vol. 4, no. 1. — P. 66—70. — doi:10.3923/ajms.2011.66.70.
- Chudnov, Alexander M. On minimax signal generation and reception algorithms (rus.) (англ.) // Problems of Information Transmission : journal. — 1986. — Vol. 22. — P. 49—54.
- Chudnov, Alexander M. Game-theoretical problems of synthesis of signal generation and reception algorithms (rus.) (англ.) // Problems of Information Transmission : journal. — 1991. — Vol. 27. — P. 57—65.