Статически определимая система
Статическая система называется статически определимой, если число неизвестных сил (внешних опорных реакций или внутренних усилий) соответствует числу уравнений статики. Количество степеней свободы такой системы равно нулю. Величины опорных реакций и внутренних усилий по принципу механического равновесия можно определить из величин внешних нагрузок.
Все другие системы называются статически неопределимыми.
Для расчёта всех статически определимых систем достаточно составления уравнений равновесия и их решения.
Для плоских задач есть три условия равновесия. Сумма всех вертикальных сил, всех горизонтальных сил и всех моментов должна быть равна нулю. Σ V=0, Σ H=0, Σ M=0.
Для пространственных задач есть шесть условий. Σ X=0, Σ Y=0, Σ Z=0, Σ Mx=0, Σ My=0, Σ Mz=0.
Осадка опор, температурные воздействия и неточности сборки в статически определимых системах не влияют на распределение и величину усилий.
Пример
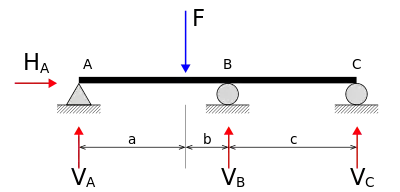
В примере справа есть 4 неизвестных реакции: VA, VB, VC и HA.
Система уравнений для их определения:
Сумма всех вертикальных сил равна 0. Σ V = 0:
- VA − Fv + VB + VC = 0
Сумма всех горизонтальных сил равна 0. Σ H = 0:
- HA − Fh = 0
Сумма всех моментов равна 0. Σ MA = 0:
- Fv · a − VB · (a + b) — VC · (a + b + c) = 0.
Поскольку неизвестных четыре (VA, VB, VC и HA) а уравнения только три, невозможно определить величину всех опорных реакций. Система следовательно статически неопределимая. Такие системы рассчитываются методами сопротивления материалов и строительной механики. Известно, например, уравнение трех моментов.
Если убрать опору B, то реакция VB исчезнет, и система становится статически определимой.
- ,
- ,
- .
Примеры простых статически определимых систем
- Консольная балка
- Балка на двух опорах