Спирограф (игрушка)

Спирограф — детская игрушка, состоит из пластмассовой пластины с вырезанными кругами разных диаметров и набора колёс меньшего диаметра с отверстиями внутри. Края кругов и колёс зубчатые, чтобы предотвратить проскальзывание. Метод использования: пластина прикладывается к листу бумаги, внутрь выбранного кругового отверстия помещается одно из зубчатых колёс, в одно из отверстий которого вставляется шариковая ручка или карандаш. Затем зубчатое колесо приводится в движение лёгким нажимом на пишущий элемент, который оставляет на бумаге спиральный след.

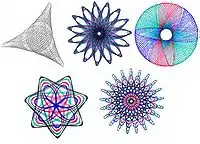
Примеры картинок, полученных с помощью спирографа.

Вместо внутреннего зубчатого колеса (круга) могут быть использованы фигуры другой формы: треугольники, овалы и т. д. Кроме того, может быть использовано несколько фигур одновременно (треугольник вращается вокруг круга, катящегося по внутренней стороне шестиугольника, или круг вращается внутри другого круга, катящегося внутри третьего круга, но в другую сторону и с другой скоростью). Это позволит получить кривые новой формы. Многие из таких кривых невозможно построить в одиночку, без помощи другого человека.

История

Спирограф, производившийся в СССР в 1980-е гг. (ОСТ 6-19-417-80 и 14МО.390.319, артикул НК-9)

Animation of a Spirograph

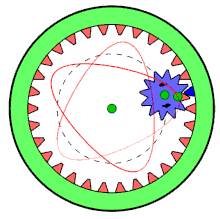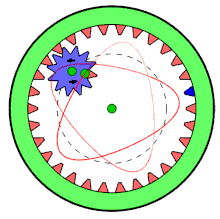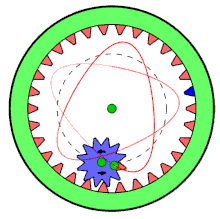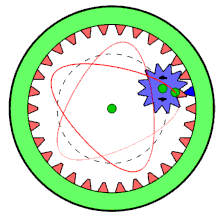
Спирограф был изобретён британским инженером Денисом Фишером (Denys Fisher) (1918—2002) в 1962 году во время работы над взрывателями для авиабомб. Ему понадобился способ быстро и точно чертить плавно изгибающиеся линии. Сделанное изобретение не помогло Дэнису продвинуться в своей работе, но оно настолько понравилось членам его семьи, что он решил выпустить его в качестве игрушки. Первые заказчики получили игрушку в 1965 году. На американский рынок «Спирограф» попал в 1966 году.

Спирограф был назван лучшей обучающей игрушкой мира четыре года подряд, с 1965 по 1969 год.

Математическое описание

Гипотрохоид с параметрами R=1,0, r=0,6, d=1,2.

Фигура, получаемая с помощью простейшего спирографа из двух кругов, когда маленький (радиуса r) с отверстием на расстоянии d от центра вращается в большом (радиуса R), называется гипотрохоидой. Её формула в декартовых координатах:

x=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)

y=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right)

См. также

Ссылки

Спирограф написанный на JavaScript. (англ.) (html). Дата обращения: 17 июня 2010. Архивировано 19 февраля 2012 года.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.