Спектральная последовательность

В гомологической алгебре и алгебраической топологии спектральная последовательность — это средство вычисления групп гомологий путём последовательных приближений. С момента их введения Жаном Лере они стали важным вычислительным средством, особенно в алгебраической топологии, алгебраической геометрии и гомологической алгебре.

Формальное определение

Зафиксируем абелеву категорию, такую как категория модулей над кольцом. Спектральная последовательность состоит из выбранного неотрицательного целого числа r₀ и набора из трёх последовательностей:

Для всех целых чисел r ≥ r₀, объектов E_r , называемых листами,
Эндоморфизмов d_r : E_r → E_r, удовлетворяющих d_r o d_r = 0, называемых граничными отображениями или дифференциалами,
Изоморфизмов E_r+1 с H(E_r), гомологией E_r относительно d_r.

Обычно изоморфизмы между E_r+1 и H(E_r) опускаются, и вместо них пишут равенства.

Простейший пример — это цепной комплекс C_•. Объект C_• из абелевой категории цепных комплексов снабжён дифференциалом d. Пусть r₀ = 0, а E₀ — это C_•. Тогда E₁ будет комплексом H(C_•): i-й член этого комплекса — это i-я группа гомологий C_•. Единственный естественный дифференциал на этом новом комплексе — это нулевое отображение, так что мы полагаем d₁ = 0. Тогда E₂ будет совпадать с E₁, и вновь единственный естественный дифференциал — это нулевое отображение. Полагая дифференциал нулевым для всех последующих листов, получаем спектральную последовательность, члены которой имеют вид:

E₀ = C_•
E_r = H(C_•) для всех r ≥ 1.

Члены этой спектральной последовательности стабилизируются с первого листа, так как единственный нетривиальный дифференциал был на нулевом листе. Следовательно, мы не получаем новой информации на последующих шагах. Обычно, чтобы получить полезную информацию из последующих листов, нужно иметь дополнительную структуру на E_r.

В неградуированной ситуации, описанной выше, r₀ не играет роли, но на практике большинство спектральных последовательностей возникает в категории дважды градуированных модулей над кольцом R (или дважды градуированных пучков модулей над пучком колец). В этом случае каждый лист является дважды градуированным модулем и раскладывается в прямую сумму членов с одним членом для каждой пары степеней. Граничное отображение определяется как прямая сумма граничных отображений на каждом члене листа. Их степень зависит от r и фиксируется соглашением. В случае гомологической спектральной последовательности члены обозначают $E_{p,q}^{r}$ и дифференциалы имеют бистепень (− r,r − 1). В случае когомологической спектральной последовательности члены обозначают $E_{r}^{p,q}$ и дифференциалы имеют бистепень (r, 1 − r). (Эти выборы степеней естественно возникают на практике; см. пример с двойным комплексом ниже.) В зависимости от спектральной последовательности, граничное отображение на первом листе имеет бистепень, соответствующую r = 0, r = 1 или r = 2. Например, для спектральной последовательности фильтрованного комплекса, описанной ниже, r₀ = 0, но для спектральной последовательности Гротендика r₀ = 2.

Пусть E_r — спектральная последовательность, начинающаяся, например, с r = 0. Тогда существует последовательность подобъектов

0=B_{0}\subset B_{1}\subset B_{2}\subset \dots \subset B_{r}\subset \dots \subset Z_{r}\subset \dots \subset Z_{2}\subset Z_{1}\subset Z_{0}=E_{0},

таких, что $E_{r}\simeq Z_{r-1}/B_{r-1}$ ; действительно, мы полагаем $Z_{0}=E_{0},B_{0}=0$ и определяем $Z_{r},B_{r}$ таким образом, что $Z_{r}/B_{r-1},B_{r}/B_{r-1}$ — это ядро и образ $E_{r}{\overset {d_{r}}{\to }}E_{r}.$

Затем мы полагаем $Z_{\infty }=\cap _{r}Z_{r},B_{\infty }=\cup _{r}B_{r}$ , тогда

E_{\infty }=Z_{\infty }/B_{\infty }

;

называется предельным членом. (Конечно, такое $E_{\infty }$ может не существовать в категории, но это обычно не является проблемой, так как, например, в категории модулей такие пределы существуют или так как спектральные последовательности, с которыми работают на практике, чаще всего вырождаются; в последовательности выше есть только конечное число включений.)

Визуализация

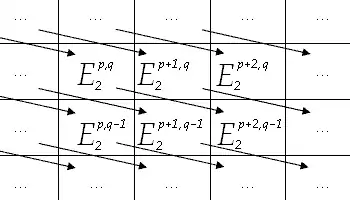
Лист E₂ когомологической спектральной последовательности

Дважды градуированная спектральная последовательность содержит большое количество данных, но существует способ визуализации, который делает структуру спектральной последовательности более понятной. Мы имеем три индекса, r, p и q. Представим, что для каждого r у нас есть лист разграфленной бумаги. На этом листе пусть p увеличивается в горизонтальном направлении, а q — в вертикальном. В каждой точке решётки мы имеем объект $E_{r}^{p,q}$ .

Как правило, n = p + q является другим естественным индексом в спектральной последовательности. n увеличивается по диагонали. В гомологическом случае дифференциалы имеют бистепень (−r, r − 1), так что они уменьшают n на 1. В когомологическом случае n увеличивается на 1. Если r нулевое, дифференциал перемещает объекты на один шаг вверх или вниз. Это напоминает дифференциал в цепном комплексе. Если r — единица, дифференциал перемещает объекты на один шаг налево или направо. Если r равно двум, дифференциал перемещает объекты сходным образом с ходом коня в шахматах. Для больших r дифференциал действует как обобщённый ход коня.

Конструкции спектральных последовательностей

Спектральная последовательность фильтрованного комплекса

Многие спектральные последовательности происходят из фильтрованных коцепных комплексов. Это коцепной комплекс C^• со множеством подкомплексов F^pC^•, где p — произвольное целое число. (На практике, p обычно ограничено с одной стороны.) Требуется, чтобы граничное отображение было согласовано с этой фильтрацией; то есть чтобы выполнялось d(F^pCⁿ) ⊆ F^pCⁿ⁺¹. Мы считаем фильтрацию убывающей, то есть F^pC^• ⊇ F^p+1C^•. Мы будем нумеровать члены коцепного комплекса индексом n. Позднее, мы будем также предполагать, что фильтрация хаусдорфова или отделима, то есть пересечение всех F^pC^• нулевое, и что фильтрация исчерпывающая, то есть объединение всех F^pC^• — это весь коцепной комплекс C^•.

Фильтрация полезна, потому что она даёт меру близости к нулю: когда p увеличивается, F^pC^• становится ближе к нулю. Мы построим спектральную последовательность из этой фильтрации, в которой кограницы и коциклы в последующих листах становятся ближе и ближе к кограницам и коциклам исходного комплекса. Эта спектральная последовательность будет дважды градуирована фильтрационной степенью p и дополнительной степенью {{{1}}}. (Дополнительная степень часто является более удобным индексом, чем n. Например, это так для спектральной последовательности двойного комплекса. описанной ниже.)

Мы построим эту спектральную последовательность вручную. C^• имеет только одну градуировку и фильтрацию, так что мы сначала построим дважды градуированный объект из C^•. Чтобы получить вторую градуировку, мы перейдём к ассоциированному градуированному объекту относительно фильтрации. Мы будем обозначать его необычным образом, что будет оправдано на шаге E₁:

Z_{-1}^{p,q}=Z_{0}^{p,q}=F^{p}C^{p+q}

B_{0}^{p,q}=0

E_{0}^{p,q}={\frac {Z_{0}^{p,q}}{B_{0}^{p,q}+Z_{-1}^{p+1,q-1}}}={\frac {F^{p}C^{p+q}}{F^{p+1}C^{p+q}}}

E_{0}=\bigoplus _{p,q\in \mathbf {Z} }E_{0}^{p,q}

Так как мы предполагали, что граничное отображение согласовано с фильтрацией, E₀ является дважды градуированным объектом и существует естественное дважды градуированное граничное отображение d₀ на E₀. Чтобы получить E₁, мы возьмём гомологию E₀.

{\bar {Z}}_{1}^{p,q}=\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}=\ker d_{0}^{p,q}:F^{p}C^{p+q}/F^{p+1}C^{p+q}\rightarrow F^{p}C^{p+q+1}/F^{p+1}C^{p+q+1}

{\bar {B}}_{1}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}/F^{p+1}C^{p+q-1}\rightarrow F^{p}C^{p+q}/F^{p+1}C^{p+q}

E_{1}^{p,q}={\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}={\frac {\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}}{{\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}}}

E_{1}=\bigoplus _{p,q\in \mathbf {Z} }E_{1}^{p,q}=\bigoplus _{p,q\in \mathbf {Z} }{\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}

Заметим, что ${\bar {Z}}_{1}^{p,q}$ и ${\bar {B}}_{1}^{p,q}$ могут быть описаны как образы в $E_{0}^{p,q}$ от

Z_{1}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+1}C^{p+q+1}

B_{1}^{p,q}=({\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}

и что мы имеем

E_{1}^{p,q}={\frac {Z_{1}^{p,q}}{B_{1}^{p,q}+Z_{0}^{p+1,q-1}}}.

$Z_{1}^{p,q}$ — это в точности то, что дифференциал перемещает на один уровень вверх по фильтрации, и $B_{1}^{p,q}$ — это в точности образ того, что дифференциал перемещает на ноль уровней вверх по фильтрации. Это подсказывает, что мы должны определить $Z_{r}^{p,q}$ как то, что дифференциал перемещает на r уровней вверх по фильтрации и $B_{r}^{p,q}$ — как образ того, что дифференциал перемещает на r-1 уровней вверх по фильтрации. Другими словами, спектральная последовательность должна удовлетворять

Z_{r}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+r}C^{p+q+1}

B_{r}^{p,q}=({\mbox{im }}d_{0}^{p-r+1,q+r-2}:F^{p-r+1}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}

E_{r}^{p,q}={\frac {Z_{r}^{p,q}}{B_{r}^{p,q}+Z_{r-1}^{p+1,q-1}}}

и мы должны иметь соотношение

B_{r}^{p,q}=d_{0}^{p,q}(Z_{r-1}^{p-r+1,q+r-2}).

Чтобы это имело смысл, мы должны найти дифференциал d_r на каждом E_r и проверить, что его гомологии изоморфны E_r+1. Дифференциал

d_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{p+r,q-r+1}

определяется как ограничение исходного дифференциала d с $C^{p+q}$ на подобъект $Z_{r}^{p,q}$ .

Нетрудно проверить, что гомологии E_r относительно этого дифференциала — это E_r+1, так что мы получаем спектральную последовательность. К сожалению, дифференциал описан не очень явно. Нахождение дифференциалов или способов обойтись без них — это одна из главных проблем, стоящих на пути успешного применения спектральной последовательности.

Спектральная последовательность двойного комплекса

Другая часто встречающаяся спектральная последовательность — это спектральная последовательность двойного комплекса. Двойной комплекс — это набор объектов C_{i, j} для всех целых i и j, вместе с двумя дифференциалами, d ^I и d ^II. По соглашению, d ^I уменьшает i и d ^II уменьшает j. Более того, мы предполагаем, что эти два дифференциала антикоммутируют, так что d ^I d ^II + d ^II d ^I = 0. Наша цель — сравнить итерированные гомологии $H_{i}^{I}(H_{j}^{II}(C_{\bullet ,\bullet }))$ и $H_{j}^{II}(H_{i}^{I}(C_{\bullet ,\bullet }))$ . Мы сделаем это, профильтровав наш двойной комплекс двумя способами. Вот наши фильтрации:

(C_{i,j}^{I})_{p}={\begin{cases}0&{\text{if }}i<p\\C_{i,j}&{\text{if }}i\geq p\end{cases}}

(C_{i,j}^{II})_{p}={\begin{cases}0&{\text{if }}j<p\\C_{i,j}&{\text{if }}j\geq p\end{cases}}

Чтобы получить спектральную последовательность, мы сведём ситуацию к предыдущему примеру. Мы определяем тотальный комплекс T(C_•,•) как комплекс, n-й член которого — это $\bigoplus _{i+j=n}C_{i,j}$ и дифференциал которого — это d ^I + d ^II. Это — комплекс, так как d ^I и d ^II — антикоммутирующие дифференциалы. Две фильтрации на C_{i, j} индуцируют две фильтрации на тотальном комплексе:

T_{n}(C_{\bullet ,\bullet })_{p}^{I}=\bigoplus _{i+j=n \atop i>p-1}C_{i,j}

T_{n}(C_{\bullet ,\bullet })_{p}^{II}=\bigoplus _{i+j=n \atop j>p-1}C_{i,j}

Чтобы показать, что эти спектральные последовательности дают информацию об итерированных гомологиях, мы опишем члены E⁰, E¹ и E² фильтрации I на T(C_•,•). Член E⁰ устроен просто:

{}^{I}E_{p,q}^{0}=T_{n}(C_{\bullet ,\bullet })_{p}^{I}/T_{n}(C_{\bullet ,\bullet })_{p+1}^{I}=\bigoplus _{i+j=n \atop i>p-1}C_{i,j}{\Big /}\bigoplus _{i+j=n \atop i>p}C_{i,j}=C_{p,q},

где n = p + q.

Чтобы найти член E¹, мы должны описать d ^I + d ^II на E⁰. Заметим, что дифференциал должен иметь степень −1 относительно n, так что мы получаем отображение

d_{p,q}^{I}+d_{p,q}^{II}:T_{n}(C_{\bullet ,\bullet })_{p}^{I}/T_{n}(C_{\bullet ,\bullet })_{p+1}^{I}=C_{p,q}\rightarrow T_{n-1}(C_{\bullet ,\bullet })_{p}^{I}/T_{n-1}(C_{\bullet ,\bullet })_{p+1}^{I}=C_{p,q-1}

Следовательно, дифференциал на E⁰ — это отображение C_p,q → C_p,q−1, индуцированное d ^I + d ^II. Но d ^I имеет неправильную степень, чтобы индуцировать такое отображение, так что d ^I должен быть нулевым на E⁰. Это значит, что дифференциал — это в точности d ^II, так что мы получаем

{}^{I}E_{p,q}^{1}=H_{q}^{II}(C_{p,\bullet }).

Чтобы найти E², мы должны определить

d_{p,q}^{I}+d_{p,q}^{II}:H_{q}^{II}(C_{p,\bullet })\rightarrow H_{q}^{II}(C_{p+1,\bullet })

Поскольку E¹ — это в точности гомология относительно d ^II, d ^II равно нулю на E¹. Следовательно, мы получаем

{}^{I}E_{p,q}^{2}=H_{p}^{I}(H_{q}^{II}(C_{\bullet ,\bullet })).

Используя другую фильтрацию, мы получаем спектральную последовательность со сходным членом E²:

{}^{II}E_{p,q}^{2}=H_{q}^{II}(H_{p}^{I}(C_{\bullet ,\bullet })).

Остаётся найти связь между этими спектральными последовательностями. Окажется, что когда r увеличивается, эти две последовательности становятся достаточно похожими, чтобы сделать полезные сравнения.

Сходимость и вырождение

В элементарном примере, с которого мы начинали, листы спектральной последовательности были постоянны, начиная с r=1. В этой ситуации имеет смысл взять предел последовательности листов: так как ничего не происходит после нулевого листа, предельный лист E_∞ — тот же, что E₁.

В более общих ситуациях предельные листы часто существуют и всегда интересны. Они являются одним из наиболее важных аспектов спектральных последовательностей. Мы говорим, что спектральная последовательность $E_{r}^{p,q}$ сходится к $E_{\infty }^{p,q}$ , если существует r(p, q), такое, что для всех r ≥ r(p, q) дифференциалы $d_{r}^{p-r,q+r-1}$ и $d_{r}^{p,q}$ нулевые. Из этого следует, что $E_{r}^{p,q}$ будет изоморфно $E_{\infty }^{p,q}$ для больших r. Это обозначается следующим образом:

E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{p,q}

Здесь p обозначает фильтрационный индекс. Часто по левую сторону сходимости пишут член $E_{2}^{p,q}$ , так как это наиболее полезный член многих спектральных последовательностей.

В большинстве спектральных последовательностей, член $E_{\infty }$ не является естественно дважды градуированным. Вместо этого, обычно существуют члены $E_{\infty }^{n}$ с естественной фильтрацией $F^{\bullet }E_{\infty }^{n}$ . В этих случаях, мы полагаем $E_{\infty }^{p,q}={\mbox{gr}}_{p}E_{\infty }^{p+q}=F^{p}E_{\infty }^{p+q}/F^{p+1}E_{\infty }^{p+q}$ . Мы определяем сходимость так же, как и раньше, но пишем

E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{n}

что означает, что когда p + q = n, $E_{r}^{p,q}$ сходится к $E_{\infty }^{p,q}$ .

Простейший случай, в котором мы можем установить сходиомость — это когда спектральная последовательность вырождается. Мы говорим, что спектральная последовательность вырождается в r-м листе, если для любого s ≥ r дифференциал d_s нулевой. Из этого следует, что E_r ≅ E_r+1 ≅ E_r+2 ≅ … В частности, из этого следует, что E_r изоморфно E_∞. Это то, что происходило в первом тривиальном примере нефильтрованного цепного комплекса: спектральная последовательность вырождалась в первом листе. В общем случае, если дважды градуированная спектральная последовательность нулевая вне горизонтальной или вертикальной полосы, спектральная последовательность вырождается, так как более поздние дифференциалы всегда входят или исходят из объекта вне полосы.

Спектральная последовательность также сходится, если $E_{r}^{p,q}$ зануляется для всех p, меньших некоторого p₀ и для всех q, меньших некоторого q₀. Если p₀ и q₀ могут быть выбраны равными нулю, это называют спектральной последовательностью первого квадранта. Эта последовательность сходится, так как каждый объект находится на фиксированном расстоянии от границы ненулевого региона. Следовательно, для фиксированных p и q, дифференциал на более поздних листах всегда отображает $E_{r}^{p,q}$ в или из нулевого объекта. Сходным образом, спектральная последовательность также сходится, если $E_{r}^{p,q}$ зануляется для всех p, больших некоторого p₀ и для всех q, больших некоторого q₀.

Литература

А. Т. Фоменко, Д. Б. Фукс. Курс гомотопической топологии. — М.: Наука, 1989. — 528 с.
Hatcher, Allen, Spectral Sequences in Algebraic Topology

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.