Смещение Малмквиста
Смещение Малмквиста (сдвиг Малмквиста) — эффект в наблюдательной астрономии, приводящий к преимущественному обнаружению объектов с высокой светимостью. Впервые данный эффект описал в 1922 году шведский астроном Гуннар Малмквист (1893—1982), подробно исследовавший данное явление в 1925 году.[1][2] В статистике данное смещение является систематической ошибкой и влияет на результаты обзоров в выборках, ограниченных по видимой звёздной величине, в которые не попадают звёзды, видимые звёздные величины которых превышают некоторое значение. Поскольку наблюдаемые звёзды и галактики кажутся слабее при большем удалении от наблюдателя, то видимая звёздная величина с расстоянием будет увеличиваться до тех пор, пока не превысит предельное значение для данного обзора. Объекты с более высокой светимостью могут наблюдаться с большего расстояния, что может создать ложную зависимость, дающую усиление блеска с расстоянием. Метод правильного учёта такого эффекта потребовал особого внимания учёных.
Теория возникновения смещения
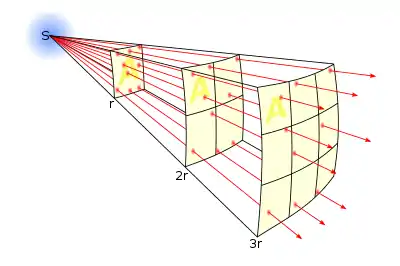
Видимая звёздная величина и блеск
Известно, что при удалении источника от наблюдателя источник выглядит всё более и более слабым. Ослабление происходит по закону обратных квадратов, утверждающему, что освещённость от источника уменьшается как 1/d2, где d равно расстоянию от источника света до наблюдателя.
Звёздный свет также распространяется по закону обратных квадратов. Лучи света распространяются в пределах сферы с центром в звезде. С течением времени сфера увеличивается, поскольку свет удаляется от звезды. Сфера увеличивается в размерах, но количество лучей остаётся неизменным. Поэтому количество света, проходящее через единичную площадку на сфере уменьшается с расстоянием и, следовательно, со временем. При наблюдении звезды только те лучи, которые попадают в пределы определённой площадки, регистрируются наблюдателем. Этот факт показывает, почему более далёкие звёзды кажутся более слабыми.
Рассмотрим две звезды одинаковой светимости, находящиеся на различном расстоянии. Более близкая звезда будет казаться более яркой. Таким образом, видимая звёздная величина зависит не только от светимости источника, но и от расстояния до него.
Если бы все звёзды обладали одинаковой светимостью, то расстояние от Земли до звезды определялось бы просто. Однако звёзды обладают существенно разными светимостями, следовательно, сложно отличить далёкую яркую звезду от слабой близкой. Таким образом, определение расстояния до астрономических объектов является сложной задачей.
Причина смещения Малмквиста
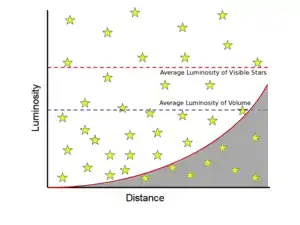
Обычно при наблюдении области неба мы можем видеть звёзды только до определённой звёздной величины. Как обсуждалось выше, нам будут видны далёкие звёзды высокой светимости и близкие звёзды, причём как яркие, так и слабые. Таким образом, будет казаться, что до определённого расстояния звёзд высокой светимости гораздо больше, чем слабых. На самом же деле, слабых звёзд гораздо больше,[3] но они не попадают в наблюдаемую выборку, поскольку слишком слабые. Смещение в сторону звёзд большей светимости при наблюдении участка неба влияет на определение среднего значения абсолютной звёздной величины и среднего расстояния до группы звёзд. Поскольку звёзды высокой светимости видны на больших расстояниях, то может казаться, что рассматриваемая выборка находится в среднем дальше, а каждая звезда вследствие этого будет считаться имеющей более высокую светимость. Данный эффект называется смещением Малмквиста.[1]
При изучении выборки источников с высокой светимостью, звёзд или галактик, важно учитывать смещение в сторону более ярких объектов. Существует несколько методов учёта влияния смещения Малмквиста.
Влияние смещения Малмквиста не ограничивается светимостями объектов. Такому же смещению подвержены и другие наблюдаемые величины, чья способность к обнаружению уменьшается с расстоянием.[4]
Методы коррекции
В идеальном случае следует не допускать данное смещение в обзорах. Однако обзоры, ограниченные по видимой звёздной величине, являются наиболее простыми для осуществления, а другие методы более сложны и требуют учёта других видов неопределённостей, что может оказаться сложным для впервые наблюдаемых объектов. Был предложен ряд различных методов, устраняющих смещение. Ниже представлены методы в порядке усложнения и повышения точности и эффективности.
Ограничение выборки
Наиболее простой метод предполагает использование только несмещённой части множества данных.[5] В зависимости от предельной звёздной величины возможен интервал значений расстояния, на которых все объекты с различными абсолютными звёздными величинами будут видны. Тогда подобное подмножество данных будет свободно от смещения Малмквиста. Получение такого подмножества можно осуществить следующим образом: предельным значением расстояния является такое, на котором наиболее слабые объекты будут обладать предельной звёздной величиной. К сожалению, данный метод предполагает исключение большого количества данных и ограничивает возможный анализ только данными о ближайших объектах. Также данный метод предполагает точное знание расстояний до объектов.
Традиционный вариант коррекции
Первое решение, предложенное Малмквистом в работе 1922 года, заключалось во внесении поправки в среднее значение абсолютной звёздной величины () выборки для получение несмещённого значения (M0).[1] Поправка равна
Для вычисления данной поправки Малмквист и другие учёные использовали ряд предположений.[6]
- Не существует межзвёздного поглощения, или же вещество между звёздами (газ или пыль) не влияет на прохождение света. Это предположение подразумевает, что распространение света подчиняется только закону обратных квадратов.
- Функция светимости (Φ) не зависит от расстояния (r). Данное предположение означает, что Вселенная одинакова в любой части и звёзды распределены в любой области так же, как и в окрестностях Солнца.
- Для заданной области на небесной сфере плотность звёзд (ρ) зависит только от расстояния, что предполагает одно и то же количество звёзд в среднем в разных направлениях.
- Выборка считается полной, то есть в ней учтены все звёзды до предельной видимой звёздной величины (mlim).
- Функцию светимости можно приблизить гауссианой с центром в средней абсолютной звёздной величине M0.
- Звёзды принадлежат одному спектральному классу, средняя абсолютная звёздная величина которого равна M0, дисперсия равна σ.
Данная ситуация является идеальной, причём последнее предположение сопряжено с наибольшими трудностями, но допускает поправку простого вида. При интегрировании функции светимости по всем расстояниям и звёздным величинам ярче mlim имеем
где A(mlim) равно полному числу звёзд ярче mlim. Если пространственное распределение звёзд можно чситать однородным, то данное соотношение упрощается и приводится к виду
Поправка в рамках наблюдений в нескольких полосах
Традиционный метод подразумевает, что измерения видимой звёздной величины и измерения, по которым осуществляется определение расстояний, проводятся в одном диапазоне длин волн (например, в полосе H, интервалу длин волн в инфракрасном диапазоне, вблизи 1300—2000 нм), что приводит к коррекции в форме cσ2, где c является константой. К сожалению, такие случаи редки, поскольку обычно расстояние до объектов определяется по наблюдениям в других диапазонах длин волн. Например, галактики часто выбираются из каталогов обзоров в полосе B, наиболее полных обзоров, и далее используются видимые звёздные величины в данной полосе, но расстояния определяются из зависимости Талли — Фишера и в полосе H. В таком случае дисперсия заменяется на ковариацию между рассеянием расстояния и рассеянием параметра галактик (например, видимой звёздной величины).[7]
Взвешивание по объёму
Другой простой метод коррекции заключается в использовании среднего взвешенного значения для учёта относительного вклада каждой величины. Поскольку объекты при разных значениях абсолютной звёздной величины могут быть видны на разных расстояниях, то вклад каждой точки в среднее значение абсолютной звёздной величины или функцию светимости можно рассматривать с весом 1/Vmax, где Vmax показывает максимальный объём, в котором могут наблюдаться объекты. Более яркие объекты (с меньшей абсолютной звёздной величиной) будут обладать большим значением объёма, в котором они могут быть обнаружены, следовательно, будут обладать меньшим весом, хотя в целом подобная группа будет представлена большим числом объектов.[8] Максимальный объём можно представить как объём сферы, радиус которой определяется из модуля расстояния по абсолютной звёздной величине объекта и предельной видимой величине.
Существуют две основные сложности при определении Vmax. Во-первых, обзор может покрывать не всё небо, то есть следует учитывать площадь части неба, где наблюдаются исследуемые объекты.[8] При полном обзоре объекты наблюдаются на всей небесной сфере, но на практике полные обзоры являются редкими вследствие временных ограничений на наблюдения, а также географических ограничений (часть неба может быть недоступна для наблюдения с определённой широты). Вместо этого проводятся наблюдения небольшого участка неба, затем предполагается определённое распределение объектов (равномерное или сгущающееся к плоскости Галактики), что позволяет экстраполировать наблюдения на всю небесную сферу. Также можно просто осуществить масштабирование количества наблюдаемых объектов по площади наблюдаемой части неба. Влияние неполноты обзора следует учитывать при сопоставлении разных обзоров.
Во-вторых, при наблюдении далёких объектов следует учитывать космологическое красное смещение и расширение Вселенной. В данном случае требуется рассматривать сопутствующее расстояние, постоянное между двумя объектами в предположении того, что они движутся относительно друг друга только вследствие расширения Вселенной. Если пренебречь расширением Вселенной, то сопутствующее расстояние можно считать расстоянием между объектами. Сопутствующее расстояние можно использовать для вычисления объёма. Если красное смещение равно z, DA и VA равны расстоянию и объёму (какими бы они были при измерении в настоящее время), DC и VC равны сопутствующему расстоянию и объёму, тогда
Серьёзным недостатком взвешивания по объёму является высокая чувствительность к крупномасштабным структурам, таким как звёздное скопление или войд.[10] Наличие участка с очень высокой или очень малой плотностью объектов внесёт существенный сдвиг в среднее значение абсолютной звёздной величины или функцию светимости. Наибольшее влияние наличие крупномасштабных неоднородностей оказывает на учёт слабых объектов, поскольку для них объёмы, в которых могут наблюдаться данные объекты, невелики.
Более сложные методы коррекции
Существует ряд более трудоёмких и корректных методов учёта смещения Малмквиста. Некоторые методы приведены ниже, дано краткое описание; более подробная информация может быть получена по ссылкам на статьи.
Коррекция на основе метода наибольшего правдоподобия
Данный способ основан на функциях распределения объектов, таких как звёзды или галактики, показывающих ожидаемое количество объектов в пределах определённого диапазона параметров. Каждый из параметров рассматриваемых объектов, такой как видимая звёздная величина, расстояние, обладает своей функцией распределения, по которой при наличии генератора случайных чисел можно создать теоретическую выборку объектов. Функция распределения расстояний считается известной, функция распределения абсолютных звёздных величин может варьироваться. Можно сопоставлять различные функции распределения абсолютной звёздной величины с наблюдаемым распределением объектов и находить такую функцию, при которой наблюдаемое распределение объектов будет наиболее вероятным. При наличии определённых ограничений на возможность обнаружения объектов можно получить настоящую несмещённую функцию распределения. Данный метод требует больших объёмов вычислений.[10][11]
Метод Шехтера
Пол Шехтер при исследовании галактик обнаружил соотношение между логарифмом ширины спектральной линии и видимой звёздной величиной.[12] В идеальном случае спектральные линии должны быть бесконечно узкими пиками, но движение объекта, такое как вращение или сдвиг по лучу зрения относительно наблюдателя приводит к уширению и смещению линий. Соотношение было найдено на основе соотношения Талли—Фишера, связывающего расстояние до галактики, видимую звёздную величину и скорость (максимальное значение на кривой вращения). Вследствие допплеровского уширения логарифм ширины наблюдаемой спектральной линии можно соотнести с шириной распределения скорости. Если считать расстояния хорошо известными, то абсолютная звёздная величина и ширина линий оказываются тесно связанными.[12] Например, при наблюдении нейтрального водорода в линии 21 см соотношение представляется в виде линейного закона
где P является логарифмом ширины спектральной линии, а α и β постоянны.
Причина, по которой данная оценка полезна, состоит в том, что линия обратной регрессии не подвержена смещению Малмквиста, эффект селекции влияет только на звёздную величину. Ожидаемое значение P при данном M будет несмещённым, что предоставит несмещённую оценку логарифма расстояния.[13]
Более сложные математические методы
Усовершенствованные варианты методов коррекции основываются на дополнительных ограничивающих предположениях. Часто такие методы приводят к сложным математическим выражениям, применимым к специфическим случаям. Например, Лури и др. вывели соотношение для смещения при наблюдении звёзд в галактике, связывающее видимую звёздную величину, абсолютную звёздную величину и высоту звезды над плоскостью галактики. Применение соотношения даёт более корректные оценки, но требует определённых предположений о пространственном распределении звёзд.[14]
Применение
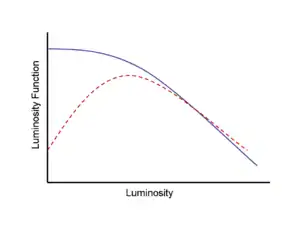
При использовании выборки с ограничением по видимой звёздной величине требуется применить один из указанных выше методов для коррекции смещения Малмквиста. Например, при получении функции светимости, калибровке зависимости Талли—Фишера или определении постоянной Хаббла смещение Малмквиста может сильно влиять на результат.
Функция светимости показывает количество звёзд или галактик в единичном интервале по светимости или абсолютной звёздной величине. При использовании выборки с ограничением по видимой звёздной величине количество слабых объектов занижается, что смещает пик функции светимости в область объектов с большей светимостью и меняет форму функции. Обычно для коррекции смещения Малмквиста используется метод взвешивания по объёму, после чего выборка считается ограниченной по расстоянию.[15] На рисунке справа представлены две функции светимости для некоторой выборки звёзд, ограниченной по видимой звёздной величине. Пунктирная кривая показывает функцию светимости без коррекции смещения Малмквиста, сплошная синяя кривая показывает скорректированную функцию светимости. Смещение Малмквиста существенно влияет на форму кривой.
Зависимость Талли—Фишера, связывающая светимость галактик со скоростью вращения, также подвержена влиянию смещения Малмквиста. Если для калибровки зависимости используется близкое скопление галактик и затем соотношение применяется к более далёкому, то расстояние до далёкого скопления будет систематически сдвинуто в меньшую сторону.[13]
Альтернативные варианты
Для того, чтобы избежать смещения Малмквиста, было придумано несколько альтернативных методов, некоторые будут представлены ниже.
Выборка, ограниченная по расстоянию
При рассмотрении выборки объектов до определённого расстояния смещение Малмквиста будет отсутствовать.[5] В такой выборке рассматриваемый объём будует включать все виды звёзд, функции распределения и функции светимости не будут искажены. На практике данный метод осуществить очень сложно, поскольку определение расстояний до объектов сопряжено с рядом трудностей. Даже в случае определения расстояния с помощью стандартных свеч полученные оценки имеют неопределённости. Чаще всего полные выборки объектов до определённого расстояния возможны только при относительно малых расстояних.
Однородная и неоднородная коррекции Малмквиста
В данном методе снова предпринимается попытка коррекции смещения, но другим способом. Вместо фиксирования абсолютных звёздных величин в методе рассматриваются расстояния до объектов как случайные величины и затем данные расстояния перемасштабируются.[13] Вместо приписывания звёздам в выборке правильного распределения по абсолютным звёздным величинам осуществляется метод сдвига объектов таким образом, чтобы распределение расстояний оказалось корректным. В идеальном случае результаты должны совпадать с результатами в методах коррекции звёздных величин. Как в однородном, так и в неоднородном методах смещение определяется в терминах априорного распределения расстояний, оценки расстояния и функции правдоподобия. В однородном случае начальные расстояния в итоге умножаются на один и тот же коэффициент. Подобный метод даёт неточный результат в случае наличия крупномасштабных структур и эффектов наблюдательной селекции. В неоднородном случае приводится попытка учесть подобные эффекты при создании более сложного априорного распределения, включающего неоднородности в наблюдаемом распределении. В обоих случаях предполагается гауссова функция распределения с постоянной дисперсией и со средним, равным истинному среднему логарифму расстояния. Границы применимости данного метода обсуждаются, поскольку при изначальном измерении расстояний до объектов присутствует ряд неопределённостей.[13]
Исторические альтернативные определения
Термин смещение Малмквиста не всегда применялся к описанному выше эффекту. Еще в 2000 году в литературе смещением Малмквиста назывался ряд статистических эффектов.[16]
Примечания
- Malmquist, Gunnar. On some relations in stellar statistics // Arkiv för Matematik, Astronomi och Fysik. — 1922. — Т. 16, № 23. — С. 1—52. — .
- Malmquist, Gunnar. A Contribution to the Problem of Determining the Distribution in Space of the Stars (англ.) // Arkiv för Matematik, Astronomi och Fysik : journal. — 1925. — Vol. 19A, no. 6. — P. 1—12. — .
- Salpeter, Edwin. The luminosity function and stellar evolution (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1955. — Vol. 121. — P. 161. — doi:10.1086/145971. — .
- Wall, J. V.; Jenkins, C. R. Practical Statistics for Astronomers. — 2nd. — Cambridge, UK: Cambridge University Press, 2012. — С. 189. — (Cambridge Observing Handbooks for Research Astronomers). — ISBN 978-0-521-73249-9.
- Sandage, Allan (November 2000), Malmquist Bias and Completeness Limits, in Murdin, P., The Encyclopedia of Astronomy and Astrophysics, Bristol: Institute of Physics Publishing, Article 1940, ISBN 0-333-75088-8, DOI 10.1888/0333750888/1940
- Butkevich, A. G.; Berdyugin, A. V.; Terrikorpi, P. Statistical biases in stellar astronomy. the Malmquist bias revisited (англ.) // MNRAS : journal. — 2005. — September (vol. 362, no. 1). — P. 321—330. — doi:10.1111/j.1365-2966.2005.09306.x. — .
- Gould, Andrew. Selection, Covariance, and Malmquist Bias (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1993. — August (vol. 412). — P. 55—58. — doi:10.1086/186939. — .
- Blanton, Michael; Schlegel, D.J.; Strauss, M.A.; Brinkmann, J.; Finkbeiner, D.; Fukugita, M.; Gunn, J.E.; Hogg, D.W.; Ivezic, Z.; Knapp, G.R.; Lupton, R.H.; Munn, J.A.; Schneider, D.P.; Tegmark, M.; Zehavi, I. New York University Value-Added Galaxy Catalog: A Galaxy Catalog Based on New Public Surveys (англ.) // The Astronomical Journal : journal. — IOP Publishing, 2005. — June (vol. 129, no. 6). — P. 2562—2578. — doi:10.1086/429803. — . — arXiv:astro-ph/0410166.
- Hogg, David W. (Dec 2000), Distance measures in cosmology, arΧiv:astro-ph/9905116
- Blanton, Michael R.; Lupton, R.H.; Schlegel, D.J.; Strauss, M.A.; Brinkmann, J.; Fukugita, M.; Loveday, J. The Properties and Luminosity Function of Extremely Low Luminosity Galaxies (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2005. — September (vol. 631, no. 1). — P. 208—230. — doi:10.1086/431416. — . — arXiv:astro-ph/0410164.
- Efstathiou, George; Frenk, C.S.; White, S.D.M.; Davis, M. Gravitational clustering from scale-free initial conditions (англ.) // MNRAS : journal. — 1988. — December (vol. 235). — P. 715—748. — doi:10.1093/mnras/235.3.715. — .
- Schechter, P.L. Mass-to-light ratios for elliptical galaxies (англ.) // Astronomical Journal : journal. — 1980. — July (vol. 85). — P. 801—811. — doi:10.1086/112742. — .
- Hendry, M.A.; Simmons, J.F.L. & Newsam, A.M. (Oct 1993), What Do We Mean by 'Malmquist Bias'?, arΧiv:astro-ph/9310028
- Luri, X.; Mennessier, M.O.; Torra, J.; Figueras, F. A new approach to the Malmquist bias (англ.) // Astronomy and Astrophysics : journal. — 1993. — January (vol. 267). — P. 305—307. — .
- Binney, James; Merrifield, Michael. Galactic Astronomy. — Princeton University Press, 1998. — С. 111—115.
- Murdin, Paul. Malmquist, Gunnar (1893–1982) // Encyclopedia of Astronomy and Astrophysics (англ.). — 2000. — ISBN 0-333-75088-8. — doi:10.1888/0333750888/3837.