Смешанный граф
Смешанный граф G = (V, E, A) представляет собой математический объект, состоящий из набора вершин (или узлов) V, набора (неориентированных) ребер E и набора направленных ребер (или дуг) A.[1]
Определения и обозначения
Дополнительная информация: Граф (математика)
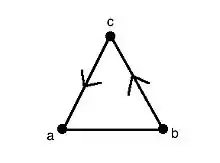
Рассмотрим соседние вершины . Ориентированным ребром, называется дуга, ребро с ориентацией, которое обозначают или (стоит заметить, что это хвост, а это голова дуги).[2] Неориентированным ребром или просто ребром, называют ребро, без ориентации и обозначают или .[2]
Дополнительная информация: Кратные рёбра
Дополнительная информация: Петля (теория графов)
В качестве нашего примера применения мы не будем рассматривать циклы или кратные ребра смешанных графов.
Маршрут в смешанном графе - это последовательность вершин и ребер/дуг, такая что для всеx индексов , элемент является ребром графа или элемент является дугой графа. Этот маршрут является путем, если в нем не повторяются ребра, дуги или вершины, кроме, возможно, первой и последней вершин. Путь является замкнутым, если его первая и последняя вершины совпадают, и замкнутый путь является циклом, если в нем не повторяются вершины, кроме первой и последней. Смешанный граф является ациклическим, если он не содержит цикла.
Раскраска
Дополнительная информация: Раскраска графов
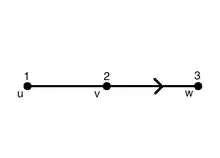
Раскраску смешанного графа можно рассматривать как маркировку или присвоение разных цветов (где - положительное целое число) вершинам смешанного графа.[3] Вершинам, соединенным ребром должны быть назначены разные цвета. Цвета могут быть представлены числами от 1 до , а для направленной дуги хвост дуги должен быть обозначен числом меньшим, чем голова дуги.[3]
Пример
Например, рассмотрим фигуру справа. Доступные нам k-цвета для окраски нашего смешанного графа: . Поскольку и связаны ребром, они должны иметь разные цвета или числа ( и помечены 1 и 2 соответственно). У нас также имеется дуга от до . Поскольку мы имеем дело с дугой, где ориентация назначает порядок чисел, мы должны пометить хвост () меньшим цветом (или целым числом из нашего набора), чем голову () нашей дуги.
Сильная и слабая раскраска
(Сильная) собственная -раскраска смешанного графа является функцией
, где такой, что , если , и , если .[1]
Мы можем ослабить условие на наши дуги. Тогда мы можем считать слабую собственную k-раскраску смешанного графа функцией
, где такой, что , если , и , если .[1] Возвращаясь к нашему примеру, это означает, что мы можем пометить голову и хвост положительным целым числом 2.
Существование
Для смешанного графа раскраска может существовать или не существовать. Для того чтобы смешанный граф имел -раскраску, он не должен содержать никаких направленных циклов.[2] Если такая -раскраска существует, то мы обозначаем наименьшее , необходимое для того, чтобы правильно раскрасить наш граф, как хроматическое число, обозначаемое .[2] Мы можем посчитать количество собственных -раскрасок как полиномиальную функцию от . Это называется хроматическим полиномом нашего графа (по аналогии с хроматическим полиномом неориентированных графов) и может быть обозначено как .[1]
Вычисление слабых хроматических полиномов
Формула удаления-стягивания может быть использована для вычисления слабых хроматических полиномов смешанных графов. Этот метод включает удаление ребра или дуги и сжатие (или соединение) оставшихся вершин, находящихся на этом ребре (или дуге), для формирования одной вершины.[1] После удаления ребра из смешанного графа мы получаем смешанный граф .[1] Мы можем обозначить это удаление ребра как . Аналогично, удаляя дугу из смешанного графа, мы получаем , где мы можем обозначить удаление as .[1] Кроме того, мы можем обозначить сокращение и как и , соответственно.[1] Из приведенных утверждений,[1] мы получаем следующие уравнения для вычисления хроматического полинома смешанного графа:
Приложения
Задача планирования
Смешанные графы могут использоваться для моделирования задач планирования работ, в которых должен выполняться сбор задач, с учетом определенных временных ограничений. В этом типе задачи ненаправленные ребра могут использоваться для моделирования ограничения того, что две задачи несовместимы (они не могут быть выполнены одновременно). Направленные ребра могут использоваться для моделирования ограничений приоритета, в которых одна задача должна быть выполнена перед другой. Граф, определенный таким образом из задачи планирования, называется дизъюнктивным графом. Смешанную задачу раскраски графов можно использовать для нахождения расписания минимальной длины для выполнения всех задач.[2]
Байесовский вывод
Смешанные графы также используются в качестве графических моделей для байесовского вывода. В этом контексте ациклический смешанный граф (без циклов направленных ребер) также называется цепным графом. Направленные ребра этих графов используются для указания причинной связи между двумя событиями, в которой исход первого события влияет на вероятность второго события. Ненаправленные ребра указывают на не причинную корреляцию между двумя событиями. Связная компонента неориентированного подграфа цепного графа называется цепочкой. Граф цепочки может быть преобразован в неориентированный граф путем построения его морального графа, неориентированного графа, сформированного из графа цепи путем добавления неориентированных ребер между парами вершин, имеющих исходящие ребра, в одну и ту же цепочку, не учитывая ориентацию направленных ребер.[4]
Примечания
- Matthias Beck, Daniel Blado, Joseph Crawford, Taïna Jean-Louis, Michael Young. On Weak Chromatic Polynomials of Mixed Graphs (англ.) // Graphs and Combinatorics. — 2015-01-01. — Vol. 31, iss. 1. — P. 91–98. — ISSN 1435-5914. — doi:10.1007/s00373-013-1381-1.
- B. Ries. Coloring some classes of mixed graphs (англ.) // Discrete Applied Mathematics. — 2007-01-01. — Vol. 155, iss. 1. — P. 1–6. — ISSN 0166-218X. — doi:10.1016/j.dam.2006.05.004.
- Pierre Hansen, Julio Kuplinsky, Dominique de Werra. Mixed graph colorings (англ.) // Mathematical Methods of Operations Research. — 1997-02-01. — Vol. 45, iss. 1. — P. 145–160. — ISSN 1432-5217. — doi:10.1007/BF01194253.
- Robert G. Cowell, Philip Dawid, Steffen L. Lauritzen, David J. Spiegelhalter. Probabilistic Networks and Expert Systems: Exact Computational Methods for Bayesian Networks. — Springer Science & Business Media, 2007-07-16. — 340 с. — ISBN 978-0-387-71823-1.
