Регистр сдвига с обобщённой обратной связью
Регистр сдвига с обобщённой обратной связью (англ. Generalized feedback shift register (GFSR)) — вариант генератора псевдослучайных чисел (ГПСЧ) Таусворта, предложенный Теодором Льюисом и Уильямом Пейном в 1973 году.
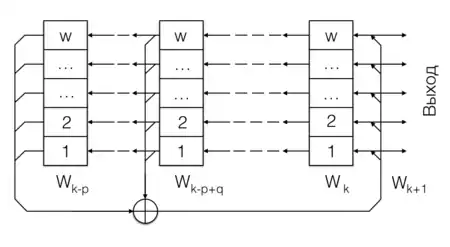
Идея алгоритма GFSR состоит в том, что основная последовательность регистра сдвига с линейной обратной связью , основанная на примитивном трёхчлене , записывается в колонок, , с разумно выбранными циклическими сдвигами. и — произвольные натуральные числа, такие что , причём примерно равных и , нужно избегать из-за плохих свойств результирующей последовательности.[1]
Таким образом все слова на выходе GFSR можно рассматривать как вектора длины , с коэффициентами из множества , которые подчиняются рекурсии
где — XOR, или побитовое сложение по модулю 2, а [2]
Сравнение с аналогичными алгоритмами
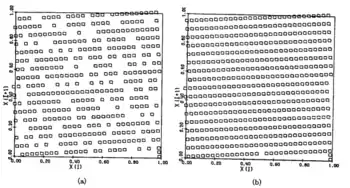
Линейный конгруэнтный генератор показывает плохую n-пространственную однородность. На рисунке предвиден пример результата работы для для 384 точек (a) и 512 (b).[1]
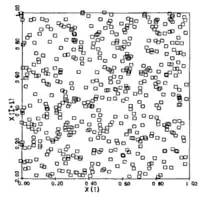
Как альтернатива, регистр сдвига с линейной обратной связью (FSR) даёт равномерное распределение в n-мерном пространстве, если длина регистра делится на n. Возможно FSR последовательности дают больше возможностей для улучшения n-мерного пространства, но период ограничен машинным словом. Кроме того, прореживание, с целью получить однородность n-мерном пространстве далее сокращает длину цикла.[1]
Из-за этого был создан регистр сдвига с обобщённой обратной связью, способный генерировать сколь угодно большие последовательности, независимо от размера машинного слова, также обладающий хорошим n-мерным распределением и большой скоростью.[1]
На рисунке предвиден пример результата работы GFSR c полиномом , 9-битным машинным словом и циклическим сдвигом на 93[1]
История исследования GFSR
Льюисом и Пейном были представлены различные типы генераторов называемые регистры сдвига с обобщённой обратной связью. Этот быстрый метод и может генерировать одинаковые последовательности на компьютерах с разной длиной машинного слова, но он имеет недостаток с инициализацией.[3]
Во-первых, невырожденная битовая начальная матрица размером должна быть сформирована. Льюис и Пейн показали, что если относительный сдвиг между соседними колонками постоянен, то матрица не вырожденная. Постоянный сдвиг был произвольно выбран равным .[3]
Во-вторых, Льюис и Пейн предложили, с целью подавить эффект неслучайности начальной матрицы, отбрасывать первые чисел перед использованием генератора. Так, если нужна длинная последовательность и большое, то процесс инициализации занимает много времени.
Другой недостаток который может быть более существенным, нет теоретического обоснования того, что последовательность будет обладать свойством k-распределения. Термин k-распределение означает, что каждый k-кортеж из -бит чисел появляется раз на полном периоде, за исключением нулевого кортежа. Они показали что последовательность может быть k-распределённая, для , но это необходимое, а не достаточное условие.[3]
Брайт (Bright) и Энисон (Enison) провели тесты на равнораспределение в пространствах большой размерности небольшой части последовательности с большим периодом. Оказалось что в тестах статистические свойства не повторяют свойства всей последовательности.[3]
Арвилиас (Arvillias) и Маритсас (Maritsas) предложили генератор типа GFSR, в которых есть степень 2. Они показали что элементов последовательности, почти равномерно распределённых вдоль периода, можно получить за один такт, используя переключатель и регистры сдвига. При этом относительный сдвиг аналитически определён. Это значит, что процесс инициализации становится столь же быстрым как и генерация случайных чисел. Но снова нет гарантий в k-распределении.[3]
Алгоритм GFSR
Входные значения:
- — задают характеристический полином регистра сдвига
- — начальная битовая последовательность
Алгоритм:
- 1. Создаем массив битовых векторов , по которому будем перемещаться с индексом и вспомогательным индексом .
- 2. Инициализируем массив, используя начальную битовую последовательность. Устанавливаем равное 0.
- 3. Вычисляем следующий вектор, но так как массив длины , то индексы вычисляются по модулю , из-за чего
- Таким образом
- 4. Увеличиваем на единицу и переходим к вычислению следующего вектора, до тех пор пока последовательность не начнет повторяться (длина последовательности )[1]
Алгоритм инициализации
- Сначала генерируется последовательность согласно алгоритму регистра сдвига с линейной обратной связью.
- После чего полученная последовательность циклически сдвигается. Величина сдвига должна быть меньше периода , тогда гарантируется что стартовые вектора будут линейно независимы (если величина сдвига взаимно просто с , то сдвиг может превышать полный период).
- Используя эту процедуру, получаем последовательностей, которые можно записать друг под другом. Первые бит последовательностей образуют матрицу, столбцы которой являются векторами [1]
Пример
Пусть дан полином , и .
Элементы последовательности удовлетворяют равенству при . Согласно полиному , так мы можем узнать элементы последовательности
и так далее.
Таким образом получаем последовательность
Для того что-бы создать хорошую случайную последовательность воспользуемся алгоритмом Кендола (Kendall). Хотя есть несколько вариантов этого алгоритма мы возьмем тот, который сдвигает начальную последовательность 1111100011011101010000100|101100 вперед на 6 бит. То есть 1011001111100011011101010|000100 и так ещё 3 раза. Таким образом получим
| Номер | последовательность |
|---|---|
| 0 | 1111100011011101010000100101100 |
| 1 | 1011001111100011011101010000100 |
| 2 | 0001001011001111100011011101010 |
| 3 | 1010100001001011001111100011011 |
| 4 | 0110111010100001001011001111100 |
образуется из первых бит последовательностей, — из вторых, для аналогично.
Последующие вычисляем согласно правилу .
| 11010 | 01001 | 00111 | |||
| 10001 | 10000 | 01111 | |||
| 11011 | 10110 | 10010 | |||
| 11100 | 10100 | 01100 | |||
| 10011 | 01110 | 00101 | |||
| 00001 | 11111 | 10101 | |||
| 01101 | 00100 | 00011 | |||
| 01000 | 11000 | 10111 | |||
| 11101 | 01011 | 11001 | |||
| 11110 | 01010 | 00110 |
Преимущества и недостатки
Преимущества
По словам разработчиков регистр сдвига с обобщённой обратной связью обладает произвольно большим периодом, независимо от длины машинного слова компьютера, который выполняет алгоритм, он быстрее чем другие генераторы псевдослучайных последовательностей, а также алгоритм легок в реализации.[1]
Недостатки
Согласно исследованиям количество 0 и 1 в выходной последовательности заметно разнится, а что противоречит постулатам Голомба. Также, если взять целое N, и разделить последовательность на кортежи по N слов, то для случайной последовательности распределение единиц в этих кортежах должно подчиняться биномиальному распределению Bin(N, 1/2). Но оказалось, что при это условие не выполняется. Это из-за того, что каждое слово зависит только от двух предыдущих, и по этому преобладание единиц или нулей не «сглаживается» сумматором по модулю 2.[2]
Вихрь Мерсенна — пример улучшения GFSR
Широко известна модификация регистра сдвига с обобщённой обратной связью под названием «Вихрь Мерсенна», предложенный Макото Мацумото и Такудзи Нисимурой в 1997 году. Период этого генератора огромен, и равен числу Мерсенна . Вихрь Мерсенна относят к классу витковых генераторов на регистрах сдвига с обобщёнными обратными связями. Его упрощённая схема приведена на рисунке
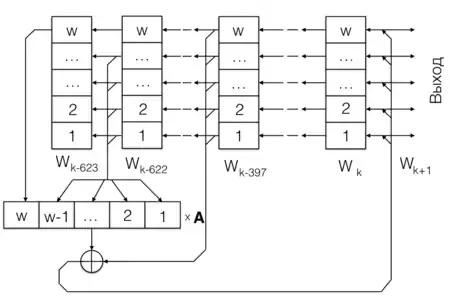
Рассмотрим наиболее распространённый вариант этого алгоритма — MT19937. Он использует 624 ячейки памяти, в каждой из которых содержится целое 32 битное число. При этом рекуррентное правило формирования последовательности выходных слов записывается таким образом:
& 0x80000000) | & 0x7fffffff))×, (i = 0, 1 , 2, …)
То есть, на каждом k-том шаге берётся старший бит слова , и 31 бит из слова , а затем полученные части конкатенируют с последующим умножением полученного результата на матрицу
где = 0x9908B0DF в шестнадцатеричном исчислении.
После этого, результат складывается по модулю 2 со словом, вычисленного на предыдущем 397-ом шаге. Затем делается сдвиг содержимого всех ячеек на шаг влево, и полученный результат записывается в освободившуюся ячейку.[2]
Литература
- T. G. Lewis, W. H. Payne. Journal of the ACM (JACM) Volume 20 Issue 3. — NY: ACM, July 1973.
- James E. Gentle. Random number generation and Monte carlo methods. — 2nd edition. — NY: Springer, 2003. — XV + 381 с. — ISBN 0-387-00178-6.
Примечания
- T. G. Lewis, W. H. Payne. Generalized Feedback Shift Register Pseudorandom Number Algorithm // J. ACM. — 1973-07-01. — Т. 20, вып. 3. — С. 456–468. — ISSN 0004-5411. — doi:10.1145/321765.321777.
- Н. Ф. Казакова, к.т.н., Ю. В. Щербина, к.т.н. ПРОБЛЕМЫ ОЦЕНКИ КАЧЕСТВА РАБОТЫ СОВРЕМЕННЫХ ЛИНЕЙНЫХ ГЕНЕРАТОРОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ (рус.) // Збірник наукових праць ОДАТРЯ No 1(2 )2013.
- M. Fushimi, S. Tezuka. The k-distribution of generalized feedback shift register pseudorandom numbers // Communications of the ACM. — 1983-07-01. — Т. 26, вып. 7. — С. 516–523. — ISSN 0001-0782. — doi:10.1145/358150.358159.