Разделённая разность

Пусть функция ${\displaystyle f}$ задана на (связном) множестве ${\displaystyle X,}$ и фиксированы попарно различные точки ${\displaystyle x_{0},\;\ldots ,\;x_{n}\in X.}$

Тогда разделённой разностью нулевого порядка функции ${\displaystyle f}$ в точке ${\displaystyle x_{j}}$ называют значение ${\displaystyle f(x_{j}),}$ а разделённую разность порядка ${\displaystyle k}$ для системы точек ${\displaystyle (x_{j},\;x_{j+1},\;\ldots ,\;x_{j+k})}$ определяют через разделённые разности порядка ${\displaystyle (k-1)}$ по формуле

${\displaystyle f(x_{j};\;x_{j+1};\;\ldots$ ;\;x_{j+k-1};\;x_{j+k})={\frac {f(x_{j+1};\;\ldots ;\;x_{j+k-1};\;x_{j+k})-f(x_{j};\;x_{j+1};\;\ldots ;\;x_{j+k-1})}{x_{j+k}-x_{j}}},}

в частности,

${\displaystyle f(x_{0};\;x_{1})={\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}},}$

${\displaystyle f(x_{0};\;x_{1};\;x_{2})={\frac {f(x_{1};\;x_{2})-f(x_{0};\;x_{1})}{x_{2}-x_{0}}}={\dfrac {{\dfrac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}-{\dfrac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}}{x_{2}-x_{0}}},}$

${\displaystyle f(x_{0};\;x_{1};\;\ldots$ ;\;x_{n-1};\;x_{n})={\frac {f(x_{1};\;\ldots ;\;x_{n-1};\;x_{n})-f(x_{0};\;x_{1};\;\ldots ;\;x_{n-1})}{x_{n}-x_{0}}}.}

Для разделённой разности верна формула

${\displaystyle f(x_{0};\;x_{1};\;\ldots$ ;\;x_{n})=\sum _{j=0}^{n}{\dfrac {f(x_{j})}{\prod \limits _{i=0 \atop i\neq j}^{n}(x_{j}-x_{i})}},}

в частности,

${\displaystyle f(x_{0};\;x_{1})={\frac {f(x_{1})}{x_{1}-x_{0}}}+{\frac {f(x_{0})}{x_{0}-x_{1}}},}$

${\displaystyle f(x_{0};\;x_{1};\;x_{2})={\frac {f(x_{2})}{(x_{2}-x_{1})(x_{2}-x_{0})}}+{\frac {f(x_{1})}{(x_{1}-x_{2})(x_{1}-x_{0})}}+{\frac {f(x_{0})}{(x_{0}-x_{2})(x_{0}-x_{1})}}.}$

Разделённая разность является симметрической функцией своих аргументов, то есть при любой их перестановке её значение не меняется, в частности,

${\displaystyle f(x_{0};\;x_{1})=f(x_{1};\;x_{0}),}$

${\displaystyle f(x_{0};\;x_{1};\;x_{2})=f(x_{1};\;x_{0};\;x_{2})=f(x_{2};\;x_{1};\;x_{0}),}$

${\displaystyle f(x_{0};\;x_{1};\;\ldots$ ;\;x_{n-1};\;x_{n})=f(x_{n};\;x_{n-1};\;\ldots ;\;x_{1};\;x_{0}).}

При фиксированной системе точек ${\displaystyle (x_{0},\;\ldots ,\;x_{n})}$ разделённая разность является линейным функционалом, то есть для функций ${\displaystyle f}$ и ${\displaystyle g}$ и скаляров ${\displaystyle a}$ и ${\displaystyle b}$:

${\displaystyle (a\cdot f+b\cdot g)(x_{0};\;\ldots$ ;\;x_{n})=a\cdot f(x_{0};\;\ldots ;\;x_{n})+b\cdot g(x_{0};\;\ldots ;\;x_{n}).}

С помощью разделённых разностей функции ${\displaystyle f}$ для узлов ${\displaystyle (x_{0},\;\ldots ,\;x_{n})}$ можно записать как интерполяционный многочлен Ньютона «вперёд»:

${\displaystyle {\begin{array}{rcl}L_{n}(x)&=&f(x_{0})+f(x_{0};\;x_{1})\cdot (x-x_{0})+f(x_{0};\;x_{1};\;x_{2})\cdot (x-x_{0})\cdot (x-x_{1})+\ldots +f(x_{0};\;\ldots$ ;\;x_{n})\cdot \prod _{k=0}^{n-1}(x-x_{k})=\\&=&f(x_{0})+(x-x_{0})\cdot \left(f(x_{0};\;x_{1})+(x-x_{1})\cdot \left(f(x_{0};\;x_{1};\;x_{2})+\ldots +(x-x_{n-1})\cdot f(x_{0};\;\ldots ;\;x_{n})\ldots \right)\right),\end{array}}}

так и интерполяционный многочлен Ньютона «назад»:

${\displaystyle {\begin{array}{rcl}L_{n}(x)&=&f(x_{n})+f(x_{n};\;x_{n-1})\cdot (x-x_{n})+f(x_{n};\;x_{n-1};\;x_{n-2})\cdot (x-x_{n})\cdot (x-x_{n-1})+\ldots +f(x_{n};\;\ldots$ ;\;x_{0})\cdot \prod _{k=1}^{n}(x-x_{k})=\\&=&f(x_{n})+(x-x_{n})\cdot \left(f(x_{n};\;x_{n-1})+(x-x_{n-1})\cdot \left(f(x_{n};\;x_{n-1};\;x_{n-2})+\ldots +(x-x_{1})\cdot f(x_{n};\;\ldots ;\;x_{0})\ldots \right)\right).\end{array}}}

Преимущества:

• для вычислений разделённых разностей требуется ${\displaystyle (n+2)(n+1)/2=O(n^{2})}$ действий (деления), что меньше, чем в других алгоритмах;
• вычислять значения интерполяционного многочлена можно по схеме Горнера за ${\displaystyle O(n)}$ действий (умножения);
• хранения требуют ${\displaystyle (n+1)}$ узел и ${\displaystyle (n+1)}$ разность, причём разности можно хранить (получить) в тех же ячейках, где были заданы значения ${\displaystyle f(x_{k})}$ ;
• по сравнению с интерполяционным многочленом Лагранжа упрощено добавление нового узла.

С использованием

${\displaystyle \left\{{\begin{array}{rcl}\omega _{j}(x)&=&(x-x_{0})\cdot \ldots \cdot (x-x_{j-1})=\prod \limits _{k=0}^{j-1}(x-x_{k})=\omega _{j-1}(x)\cdot (x-x_{j-1}),\;j>0,\\\omega _{0}(x)&=&1\end{array}}\right.}$

первую из формул можно записать в виде

${\displaystyle L_{n}(x)=\sum _{j=0}^{n}f(x_{0};\;\ldots$ ;\;x_{j})\cdot \omega _{j}(x).}

С помощью многочлена Ньютона можно также получить следующее представление разделённых разностей в виде отношения определителей:

${\displaystyle f(x_{0};\ldots ;x_{n})={\frac {\left|{\begin{array}{ccccc}1&x_{0}&\ldots &x_{0}^{n-1}&f(x_{0})\\\vdots &\vdots &\ddots &\vdots &\vdots \\1&x_{n}&\ldots &x_{n}^{n-1}&f(x_{n})\end{array}}\right|}{\left|{\begin{array}{ccccc}1&x_{0}&\ldots &x_{0}^{n-1}&x_{0}^{n}\\\vdots &\vdots &\ddots &\vdots &\vdots \\1&x_{n}&\ldots &x_{n}^{n-1}&x_{n}^{n}\end{array}}\right|}}.}$

Ньютон использовал в своей общей формуле интерполяции (см. выше) разделённые разности, но термин, по-видимому, был введён О. де Морганом в 1848 году[1].

Пример для функции ${\displaystyle f(x)=2x^{3}-2x^{2}+3x-1}$

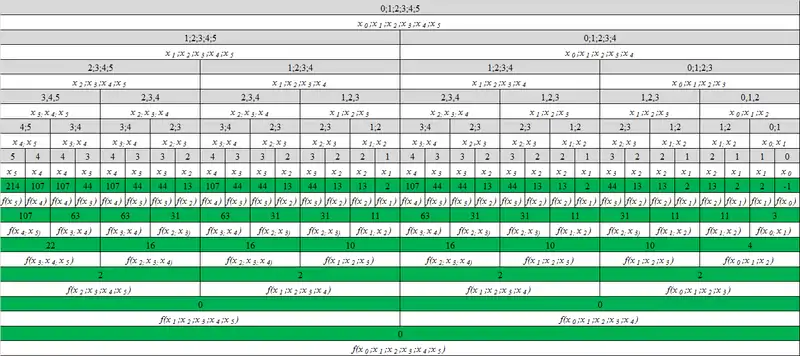
На приведённом изображении рассмотрен пример вычисления разделённых разностей для

${\displaystyle {\begin{array}{rcl}f(x)&=&2x^{3}-2x^{2}+3x-1,\\x_{i}&=&i,\;i=0,\ldots ,n,\\n&=&5.\end{array}}}$

• Конечные разности
• Численное дифференцирование

• Интерполирование Эрмита с использованием разделенных разностей.

• Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. — 3-е изд., доп. и перераб. — М.: БИНОМ. Лаборатория знаний, 2004. — 636 с., илл. — ISBN 5-94774-175-X.
• Корн Г. (Granino A. Korn, Ph.D.), Корн Т. (Theresa M. Korn, M.S.) Справочник по математике (для научных работников и инженеров) (англ. Mathematical handbook for scientist and engineers, 1968). — М.: Наука, 1973. — 832 с., илл.