Птолемеев граф
В теории графов птолеме́ев граф — это неориентированный граф, в котором расстояния по кратчайшему пути удовлетворяют неравенству Птолемея (греческого астронома и математика Птолемея). Птолемеевы графы — это в точности графы, которые одновременно являются и хордальными, и дистанционно наследуемыми. Эти графы включают блоковые графы[1] и являются подклассом совершенных графов.
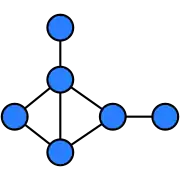
Птолемеев граф
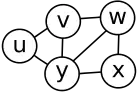
Граф-изумруд (или 3-веер) не птолемеев.

Блоковый граф, специальный вид птолемеевых графов
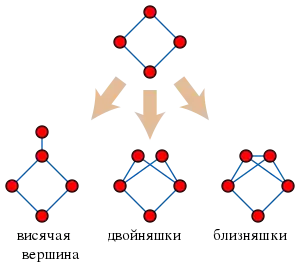
Три операции, с помощью которых может быть построен любой дистанционно-наследуемый граф. Для птолемеевых графов соседи двойняшек должны образовывать клику, чтобы предотвратить построение 4-цикла, показанного здесь.
Описание
Граф является птолемеевым тогда и только тогда, когда он удовлетворяет следующим эквивалентным условиям:
- Расстояния по кратчайшему пути удовлетворяют неравенству Птолемея — для любых четырёх вершин u, v, w и x выполняется неравенство d(u,v)d(w,x) + d(u,x)d(v,w) ≥ d(u,w)d(v,x)[1]. Например, граф-изумруд (3-веер) на рисунке не является птолемеевым, поскольку в этом графе d(u,w)d(v,x) = 4 больше, чем d(u,v)d(w,x) + d(u,x)d(v,w) = 3.
- Для любых перекрывающихся максимальных клик их пересечение является сепаратором, который разделяет разность этих двух клик[2]. Для графа-изумруда на иллюстрации это не так — клики uvy и wxy не разделяются их пересечением y, поскольку существует ребро vw, соединяющее клики.
- Любой цикл с k вершинами имеет по меньшей мере 3(k − 3)/2 диагоналей[2].
- Граф является и хордальным (любой цикл с длиной, превосходящей три, имеет диагональ), и дистанционно-наследуемым (любой связный порождённый подграф имеет те же расстояния, что и весь граф)[2]. Граф-изумруд является хордальным, но не дистанционно-наследуемым — в подграфе, порождённом uvwx, расстояние от u до x равно 3, что больше, чем расстояние между теми же вершинами в полном графе. Поскольку как хордальные, так и дистанционно-наследуемые графы являются совершенными, таковыми же являются и птолемеевы графы [3].
- Граф хордален и не содержит изумрудов — графов, образованных добавлением двух непересекающихся диагоналей в пятиугольник [3].
- Граф является дистанционно-наследуемым и не содержит порождённых 4-циклов[4].
- Граф может быть построен из единственной вершины последовательностью операций, при которых добавляется новая вершина степени 1 (висячая) или дублируется существующая вершина (образуя близняшки или двойняшки), с условием, что операция удвоения, в которой дубликат вершины не смежен своей паре (двойняшки), только если соседи этих удвоенных вершин образуют клику. Эти три операции, если не применять указанное условие, образуют все дистанционно-наследуемые графы. Для образования птолемеевых графов недостаточно использовать образование висячих вершин и близняшек, образование двойняшек (при соблюдении указанных выше условий) тоже иногда требуется[5].
- Диаграмма Хассе подмножества отношений непустого пересечения максимальных клик образует ориентированное дерево[6].
- Выпуклые подмножества вершин (подмножества, содержащие все кратчайшие пути между двумя вершинами в подмножестве) образуют выпуклую геометрию. То есть любое выпуклое множество может быть получено из полного набора вершин последовательным удалением крайних вершин, то есть не принадлежащих какому-либо кратчайшему пути между оставшимися вершинами[7]. В изумруде выпуклое множество uxy не может быть получено таким способом, поскольку ни v, ни w не являются крайними.
Вычислительная сложность
Основываясь на описании ориентированными деревьями, птолемеевы графы можно распознать за линейное время[6].
Примечания
- Kay, Chartrand, 1965, p. 342–346.
- Howorka, 1981, p. 323–331.
- Graphclass: ptolemaic, <http://www.graphclasses.org/classes/gc_95.html>. Проверено 5 июня 2016..
- McKee, 2010, p. 651–661.
- Bandelt, Mulder, 1986, p. 182–208.
- Uehara, Uno, 2009, p. 1533–1543.
- Farber, Jamison, 1986, p. 433–444.
Литература
- Hans-Jürgen Bandelt, Henry Martyn Mulder. Distance-hereditary graphs // Journal of Combinatorial Theory. — 1986. — Vol. 41, no. 2. — P. 182–208. — doi:10.1016/0095-8956(86)90043-2.
- Martin Farber, Robert E. Jamison. Convexity in graphs and hypergraphs // SIAM Journal on Algebraic and Discrete Methods. — 1986. — Vol. 7, no. 3. — P. 433–444. — doi:10.1137/0607049.
- Edward Howorka. A characterization of Ptolemaic graphs // Journal of Graph Theory. — 1981. — Vol. 5, no. 3. — P. 323–331. — doi:10.1002/jgt.3190050314.
- David C. Kay, Gary Chartrand. A characterization of certain ptolemaic graphs // Canadian Journal of Mathematics. — 1965. — Vol. 17. — P. 342–346. — doi:10.4153/CJM-1965-034-0.
- Terry A. McKee. Clique graph representations of Ptolemaic graphs // Discussiones Mathematicae Graph Theory. — 2010. — Vol. 30, no. 4. — P. 651–661. — doi:10.7151/dmgt.1520.
- Ryuhei Uehara, Yushi Uno. Laminar structure of Ptolemaic graphs with applications // Discrete Applied Mathematics. — 2009. — Vol. 157, no. 7. — P. 1533–1543. — doi:10.1016/j.dam.2008.09.006.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
