Предел упругости
Предел упругости (англ. Elastic limit) — свойство вещества, максимальное напряжение нагрузки, после снятия которой не возникает остаточных (пластических)[1] деформаций[2]. Применяется в теории упругости, сопротивлении материалов. В ДСТУ 2825-94 назван границей упругости[3].
Описание
Предел упругости принято определять величиной напряжения при допускаемой малой деформации и, соответственно, измерять в паскалях[4].
где σy — предел упругости[Па], FY [Н]— нагрузка, S0 [м2]— площадь образца при допускаемой остаточной деформации. У большинства тел предел упругости и предел пропорциональности совпадают[3].
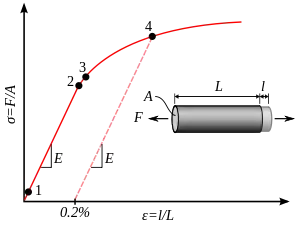
За пределом упругости график «напряжение/деформация» (деформационная кривая) отклоняется от прямой[5]. Предел упругости существует как для деформации растяжения, так и при сжатии[1]. В общем случае эти пределы различны и могут отличаться вдоль различных осей приложения нагрузки[6][7].Более того, выход за предел упругости при сжатии приводит к изменению предела упругости на растяжение и наоборот. Это явление называется эффектом Баушингера[1].
Под действием длительной нагрузки твёрдое тело приобретает ползучесть (иначе текучесть) — пластические деформации при напряжениях внешней силы до предела упругости. Это явление характерно для пластов горных пород[8].
При некоторых условиях превышающие предел упругости нагрузки приводят к увеличению последнего[9]. Такое повышение называется наклёпом или упрочнением[1].
Примечания
- Белов Н. Н., 2008.
- Ляв, 2013.
- Предел упругости. nado.znate.ru. Дата обращения: 15 января 2017.
- Бегун П. И., Кормилицын О. П., 2017.
- Д. Джанколи.
- Уманский А. А..
- Рычков Б. А., Комарцов Н. М., Лужанская Т. А. О ПРЕДЕЛАХ УПРУГОСТИ И ПРОЧНОСТИ ГОРНЫХ ПОРОД (рус.) // ВЕСТНИК ПНИПУ Механика : статья в журнале. — 2013. — № 2. — С. 110—123.
- Салихов В. С., 2015.
- Техническая энциклопедия, 2013.
Литература
- Ляв А. Математическая теория упругости. — Directmedia, 2013. — 671 с.
- Техническая энциклопедия. — Directmedia, 2013. — 440 с.
- Бегун П. И., Кормилицын О. П. Прикладная механика. — Litres, 2017. — 473 с.
- Д. Джанколи. Физика. — Рипол Классик.
- Белов Н. Н. Т. 2 : Введение в механику сплошной среды. Уравнения гиперболического типа. — STT Publishing, 2008. — 330 с.
- Салихов В. С. Словарь основных терминов и понятий по геологии: Учебное пособие. — Scientific magazine "Kontsept", 2015. — С. 22. — 143 с.
- Уманский А. А. Справочник проектировщика расчетно-теоретический. — Рипол Классик.