Периферийный цикл

Периферийный цикл в неориентированном графе — цикл, который, не отделяет любую часть графа от любой другой. Периферийные циклы (или, как они сначала назывались, периферийные многоугольники, поскольку Татт называл циклы «многоугольниками»), первым изучал Татт, Уильям Томас[1]. Они играют важную роль в описании планарных графов и в образовании циклических пространств непланарных графов[2].

В этом графе красный треугольник, образованный вершинами 1, 2 и 5 является периферийным циклом — четыре оставшихся ребра образуют отдельный мост. Однако, пятиугольник 1-2-3-4-5 не является периферийным, поскольку два оставшихся ребра образуют два отдельных моста.

Определения

Периферийный цикл в графе можно определить формально одним из следующих способов:

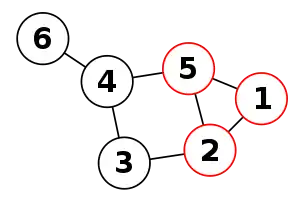
  • является периферийным циклом, если он является простым циклом в связном графе со свойством, что для любых двух рёбер и в , существует путь в , который начинается в , кончается в и не имеет внутренних точек, принадлежащих [3].
  • является периферийным циклом, если он является порождённым циклом со свойством, что подграф , образованный удалением рёбер и вершин цикла связен.[4]
  • Если является любым подграфом графа , мост[5] графа является минимальным подграфом графа , не имеющим общих рёбер с и имеющим свойство, что все его точки присоединения (вершины, смежные рёбрам, принадлежащим и одновременно) принадлежит [6]. Простой цикл является периферийным, если он имеет в точности один мост[7]

Эквивалентность этих определений нетрудно видеть: связный подграф графа (вместе с рёбрами, связывающими его с ) или хорда цикла, которая нарушает порождение цикла, в любом случае должен быть мостом и должен быть также класс эквивалентности бинарного отношения на рёбрах, в котором два ребра связаны, если они являются концами пути без внутренних вершин в [8]

Свойства

Периферийные циклы появляются в теории полиэдральных графов, то есть, вершинно 3-связных планарных графов. Для любого планарного графа и любого планарного вложения грани вложения, порождённые циклами, должны быть периферийными циклами. В полиэдральном графе все грани являются периферийными циклами и любой периферийный цикл является гранью[9]. Отсюда следует, что (до комбинаторной эквивалентности, выбора внешней грани и ориентации плоскости) любой полиэдральный граф имеет уникальное планарное вложение[10].

В планарных графах циклическое пространство, образованное гранями, но в непланарных графах периферийные циклы играют аналогичную роль — для любого вершинно 3-связанного конечного графа циклическое пространство образуется периферийными циклами[11]. Результат можно распространить на локально конечные бесконечные графы[12]. В частности, отсюда следует, что 3-связные графы гарантированно содержат периферийные циклы. Существуют 2-связные графы, которые не содержат периферийные циклы (примером является полный двудольный граф , в котором любой цикл имеет два моста), но если 2-связный граф имеет минимальную степень три, то он содержит по меньшей мере один периферийный цикл[13].

Периферийные циклы в 3-связных графах могут быть вычислены в линейное время и использовались для разработки тестов планарности[14]. Они были также расширены до более общего понятия не разделяющих ушных разложений. В некоторых алгоритмах для проверки планарности графов полезно найти цикл, который не является периферийным, с целью разбиения задачи на меньшие подзадачи. В двусвязном графе с контурным рангом, меньшим трёх, (таком как цикл или тета-граф), любой цикл является периферийным, но любой двусвязный граф с контурным рангом три и более имеет не периферийный цикл, который может быть найден за линейное время[15].

Обобщая хордальные графы, Сеймур и Вивер [16] определили сжатый граф как граф, в котором любой периферийный цикл является треугольником. Они описали эти графы как суммы по кликам хордальных графов и максимальных планарных графов[17].

Связанные понятия

Периферийные циклы назывались также не разделяющими циклами[3], но этот термин двусмысленный, поскольку он используется еще для двух других понятий — для простых циклов, удаление которых делает оставшийся граф несвязным[18], и для циклов топологического вложения графа, таких что вырезание вдоль цикла не делает несвязной поверхность, в которую граф вложен[19].

В матроидах, не разделяющий цикл — это цикл матроида (то есть, минимальное зависимое множество), такое что удаление цикла оставляет меньший матроид, который связан (то есть, который не может быть разбит на прямую сумму матроидов)[20]. Они аналогичны периферийным циклам, но не то же самое даже в графовых матроидах (матроиды, в которых циклы являются простыми циклами графа). Например, в полном двудольном графе любой цикл является периферийным (он имеет лишь один мост, путь из двух рёбер), но графовый матроид, образованный этим мостом не связен, так что никакой цикл графового матроида графа не является не разделяющим.

Примечания
  1. Tutte, 1963.
  2. Tutte, 1963, с. 743–767.
  3. Di Battista, Eades, Tamassia, Tollis, 1998, с. 74–75.
  4. Это определение, которое использовал Брун (Bruhn 2004). Однако, Брун различал случай, что имеет изолированные вершины от несвязности, вызванной удаления цикла .
  5. Не путать с мостом, другим понятием с тем же названием.
  6. Tutte, 1960, с. 304–320.
  7. Это определение периферийных циклов первоначально использовал Татт(Tutte 1963). Сеймур и Вивер(Seymour, Weaver 1984) использовал то же определение периферийного цикла, но с другим определением моста, которое ближе напоминает определение порождённых циклов для периферийных циклов.
  8. См., например, теорему 2.4 в статье Татта (Tutte 1960), показывющую, что множество вершин мостов связаны путями, см. статью Сеймур и Вивера (Seymour, Weaver 1984) для определения мостов с помощью хорд и связных компонент, а также статью Ди Баттиста, Идса, Тамассиа, Толлиса(Di Battista, Eades, Tamassia, Tollis 1998) для определения мостов с помощью классов эквивалентности бинарного отношения на рёбрах.
  9. Tutte, 1963, с. Theorems 2.7 и 2.8.
  10. См. замечания после теоремы 2.8 в статье Татта (Tutte 1963). Как замечает Татт, это было уже известно Уитни (Whitney 1932)
  11. Tutte, 1963, с. Theorem 2.5.
  12. Bruhn, 2004, с. 235–256.
  13. Thomassen, Toft, 1981, с. 199–224.
  14. Schmidt, 2014, с. 967—978.
  15. Di Battista, Eades, Tamassia, Tollis, 1998, с. 75–76 Lemma 3.4.
  16. Seymour, Weaver, 1984.
  17. Seymour, Weaver, 1984, с. 241–251.
  18. См., например, (Borse, Waphare 2008)
  19. См, например (Cabello, Mohar 2007)
  20. Maia, Lemos, Melo, 2007, с. 162–171.

Литература
  • Tutte W. T. How to draw a graph // Proceedings of the London Mathematical Society. — 1963. — Т. 13. — С. 743–767. — doi:10.1112/plms/s3-13.1.743.
  • Giuseppe Di Battista, Peter Eades, Roberto Tamassia, Ioannis G. Tollis. Graph Drawing: Algorithms for the Visualization of Graphs. — Prentice Hall, 1998. — С. 74–75. — ISBN 978-0-13-301615-4.
  • Tutte W. T. Convex representations of graphs // Proceedings of the London Mathematical Society. — 1960. — Т. 10. — С. 304–320. — doi:10.1112/plms/s3-10.1.304.
  • Hassler Whitney. Non-separable and planar graphs // Transactions of the American Mathematical Society. — 1932. — Т. 34, вып. 2. — С. 339–362. — doi:10.2307/1989545.
  • Henning Bruhn. The cycle space of a 3-connected locally finite graph is generated by its finite and infinite peripheral circuits // Journal of Combinatorial Theory. — 2004. — Т. 92, вып. 2. — С. 235–256. — doi:10.1016/j.jctb.2004.03.005.
  • Carsten Thomassen, Bjarne Toft. Non-separating induced cycles in graphs // Journal of Combinatorial Theory. — 1981. — Т. 31, вып. 2. — С. 199–224. — doi:10.1016/S0095-8956(81)80025-1.
  • Jens M. Schmidt. The Mondshein Sequence // Proceedings of the 41st International Colloquium on Automata, Languages and Programming (ICALP'14). — 2014. — С. 967—978. — doi:10.1007/978-3-662-43948-7_80.
  • Seymour P. D., Weaver R. W. A generalization of chordal graphs // Journal of Graph Theory. — 1984. — Т. 8, вып. 2. — С. 241–251. — doi:10.1002/jgt.3190080206.
  • Borse Y. M., Waphare B. N. Vertex disjoint non-separating cycles in graphs // The Journal of the Indian Mathematical Society. — 2008. — Т. 75, вып. 1—4. — С. 75–92 (2009).
  • Sergio Cabello, Bojan Mohar. Finding shortest non-separating and non-contractible cycles for topologically embedded graphs // Discrete and Computational Geometry. — 2007. — Т. 37, вып. 2. — С. 213–235. — doi:10.1007/s00454-006-1292-5.
  • Bráulio Maia Junior, Manoel Lemos, Tereza R. B. Melo. Non-separating circuits and cocircuits in matroids // Combinatorics, complexity, and chance. — Oxford: Oxford Univ. Press, 2007. — Т. 34. — С. 162–171. — (Oxford Lecture Ser. Math. Appl.). — doi:10.1093/acprof:oso/9780198571278.003.0010.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.