Периодограмма
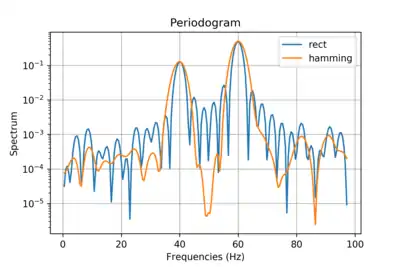
Периодограмма — оценка спектральной плотности мощности (СПМ), основанная на вычислении квадрата модуля преобразования Фурье последовательности данных. Если при расчёте СПМ используется весовая функция (окно), то полученная оценка СПМ называется модифицированной периодограммой[1]. Периодограмма не является состоятельной оценкой СПМ, поскольку дисперсия такой оценки сравнима с квадратом её математического ожидания. С ростом числа используемых отсчётов значения периодограммы начинают всё быстрее флуктуировать.
Математическое описание
В литературе существует несколько определений термина периодограмма. Одно из них связано с усреднением квадрата модуля преобразования Фурье по некоторой выборке измерений[2]:
где — амплитуда преобразования Фурье функции на конечном временном интервале, — интервал финитности, — оператор статистического усреднения (математическое ожидание).
Однако, в англоязычной литературе[3] и в популярных программных реализациях[4][5], как правило, подразумевается просто квадрат модуля амплитуды преобразования Фурье. Временное усреднение в таких классификациях отводится методам Бартлетта и Уэлча[6].
Исторические сведения
Термин периодограмма впервые был упомянут Артуром Шустером в 1898[8] году. Шустер применил периодограмму для отыскания периодичностей в записях метеорологических наблюдений, записях магнитного склонения и ряда чисел солнечных пятен. Он выполнил предварительную обработку среднемесячных значений числа солнечных пятен за период с 1749 по 1894 год. Периодограммный анализ позволил дать оценку цикла солнечных пятен, равную 11,125 года. Шустер указал многочисленные трудности, связанные с вычислением периодограммы, и характерные её особенности. Изменяя начало отсчёта времени, он получал образцы периодограммы с различными нерегулярными изменениями, причём эти периодограммы иногда содержали ложные пики (Шустер называл их «случайными периодичностями») там, где в действительности никакой периодичности не существовало. Шустер из своего опыта гармонического анализа оптических спектров знал, что усреднение значений, полученных для различных отрезков последовательности данных, необходимо для сглаживания периодограммы (получения «средней периодограммы» в его терминологии) и устранения ложных пиков. И хотя Шустер установил необходимость усреднения, практическая его реализация требовала вычислительных средств, далеко выходящих за рамки имеющихся в те годы технических возможностей. Шустер также понимал, что боковые лепестки (которые он называл «ложными периодичностями») вокруг главных лепестков в периодограмме являются неотъемлемой особенностью любого метода анализа Фурье записей данных конечной длины.
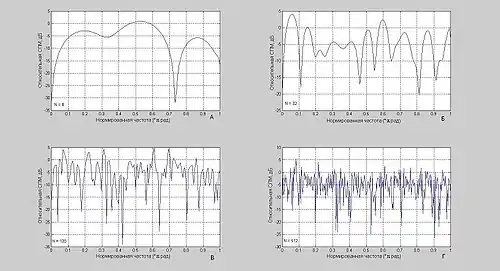
Многие исследователи начала прошлого столетия считали, что периодограммы, вычисленные по зашумлённым данным, будут иметь значительные погрешности и вообще не будут содержать каких-либо доминирующих пиков, которые могли бы свидетельствовать о наличии периодичностей в анализируемых данных. Причём это считалось справедливым даже тогда, когда длина записи данных существенно возрастала. Примеры таких периодограмм показаны на рисунке, из которого видно, что с использованием всё большего и большего числа отсчётов данных периодограмма начинает всё сильнее и сильнее флуктуировать. Всё это привело к тому, что на несколько десятилетий интерес к периодограммам значительно ослабел, и это в основном можно объяснить лишь тем, что большинство исследователей пренебрегало усреднением, использовать которое предлагал Шустер. Слуцкий и несколько позднее Даньелл независимо установили, что флуктуации периодограммы белого шума имеют ту же величину, что и среднее значение самой этой периодограммы. Эти флуктуации оказывались в основном некоррелированными для соседних частот. Слуцкий и Даньелл высказали предположение, что флуктуации периодограммы можно уменьшить посредством её усреднения по соседним частотам. Эта идея лежит в основе одного из методов сглаживания периодограммы.
Литература
- Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения. — М.: МИР, 1990. — С. 584.Архивная копия от 24 января 2009 на Wayback Machine
- Hayes M. H. Statistical digital signal processing and modeling. — John Wiley & Sons, 2009.
- Айфичер Э., Джервис Б. Цифровая обработка сигналов: практический подход. — 2-е. — М.: Вильямс, 2004. — С. 992. — ISBN 5-8459-0710-1 (рус.).
- Шахтарин Б. И., Ковригин В. А. Методы спектрального оценивания случайных процессов. — М.: Гелиос АРВ, 2005. — С. 248. — ISBN 5-85438-136-2.
- Сергиенко А. Б. Цифровая обработка сигналов. — 2-е. — СПб.: Питер, 2006. — С. 751. — ISBN 5-469-00816-9.
Ссылки
- Hayes, 2009, с. 408-412.
- Марпл-мл. С. Л., 1990, с. 190.
- Hayes, 2009, с. 394.
- scipy.signal.periodogram
- periodogram (MathWorks)
- scipy.signal.welch
- Марпл-мл. С. Л., 1990, с. 22.
- Schuster, A., "On the investigation of hidden periodicities with application to a supposed 26 day period of meteorological phenomena, " Terrestrial Magnetism and Atmospheric Electricity, 3, 13-41, 1898.