Непредикативность (математика)

Непредикати́вность определения в математике и логике, нестрого говоря, означает, что осмысленность определения предполагает наличие определяемого объекта[1]. Пример: объект определяется как такой элемент некоторого множества, который удовлетворяет определённому отношению между ним и всеми элементами этого множества (включая и само )[2]. В некоторых случаях непредикативное определение может привести к недоразумениям или даже противоречиям. Противоположное по смыслу понятие — предикативность.

Для определений на формальном языке «Математическая энциклопедия» приводит более строгий вариант:

Свойство (точнее, языковое выражение, выражающее это свойство) называется непредикативным, если оно содержит связанную переменную, в область изменения которой попадает определяемый объект. Свойство называется предикативным, если оно не содержит таких связанных переменных.

Не существует общепризнанного чёткого определения непредикативности, различные источники дают сходные, но разные определения. Например, встречается такое: определение объекта X непредикативно, если оно либо ссылается на само X, либо (чаще всего) на множество , содержащее X; при этом представляется законченным, хотя данное определение может повлиять на его состав[3][4].

Примеры

Наиболее известный пример непредикативного построения — парадокс Рассела, в котором определяется совокупность всех множеств, не содержащих самих себя. Парадокс заключается в том, что так определённое множество внутренне противоречиво — оно одновременно и содержит себя, и не содержит. Наглядный исторический вариант этого парадокса — «парадокс брадобрея»: определение «житель деревни, который бреет тех жителей этой деревни, которые не бреются сами», является непредикативным, так как определяет жителя деревни, используя его отношения со всеми жителями деревни (а, значит, и с ним самим)[2]. Непредикативность обнаруживается и в других парадоксах теории множеств[3].

Парадокс всемогущества

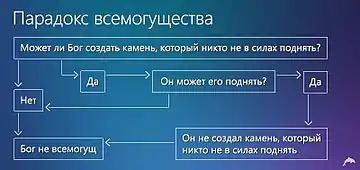
К непредикативным формулировкам часто относят и парадокс всемогущества: «Может ли Бог создать камень, который он сам не сможет поднять?» Здесь используется понятие «всемогущество», определение которого внутренне противоречиво[5]. Аналогично устроен «парадокс лжеца», в котором утверждение отрицает само себя.

В математике существует, однако, немалое количество часто используемых непредикативных определений, не создающих проблем и не имеющих простого предикативного варианта. В классическом анализе, например, таково определение точной нижней грани числового множества[6]:

Точной (наибольшей) нижней гранью подмножества упорядоченного множества называется наибольший элемент , который не превосходит всех элементов множества

Другой пример общепринятого и вполне безопасного непредикативного определения в анализе — определение максимального значения функции на заданном интервале, поскольку определяемое значение зависит от всех прочих, включая самого себя[7].

Непредикативные конструкции использует доказательство знаменитой теоремы Гёделя о неполноте: построенная в итоге «неразрешимая формула» утверждает недоказуемость самой себя[8].

Наконец, в логике и информатике существуют рекурсивные определения и рекурсивные алгоритмы, в которых непредикативность изначально предусмотрена и является их неотъемлемой составной частью.

История

Термины «предикативный» и «непредикативный» были введены в статье Рассела (1907)[9], хотя смысл термина тогда был несколько иным. Как опасный порочный круг непредикативные определения осудил Анри Пуанкаре (1905—1906, 1908), он считал их главным источником парадоксов теории множеств. Рассел поддержал эту оценку и в своей монографии «Principia Mathematica» принял меры по недопущению непредикативности (теория типов и «аксиома сводимости»)[10][11]. Герман Вейль в своей книге «Das Kontinuum» изложил философскую позицию, которую часто называют «предикативизм»[12].

Эрнст Цермело в 1908 году выступил с возражениями против чрезмерно радикального подхода и привёл два примера вполне безобидных непредикативных определений, часто используемых в анализе. Герман Вейль попытался найти предикативный аналог определения наименьшей верхней грани, но успеха не добился. С тех пор никому так и не удалось построить анализ в полном объёме на строго предикативной основе[1][3].

Примечания
  1. Математическая энциклопедия, 1982, с. 981.
  2. Непредикати́вное определе́ние Архивная копия от 3 февраля 2018 на Wayback Machine // Большая Российская энциклопедия.
  3. Клини С. К. Введение в метаматематику. — М.: Изд-во иностранной литературы, 1957. — С. 44—46. — 526 с.
  4. Философский энциклопедический словарь, 1983, с. 433.
  5. Клайн М., 1984, с. 241.
  6. Клайн М., 1984, с. 241—242.
  7. Клайн М., 1984, с. 242.
  8. Успенский В. А. Теорема Гёделя о неполноте. — М.: Наука, 1982. — 110 с. — (Популярные лекции по математике).
  9. Russell, B. (1907), On some difficulties in the theory of transfinite numbers and order types. Proc. London Math. Soc., s2-4 (1): 29-53, doi:10.1112/plms/s2-4.1.29.
  10. Feferman, Solomon. Predicativity Архивная копия от 11 июня 2016 на Wayback Machine (2002)
  11. Willard V. Quine’s commentary before Bertrand Russell’s 1908 Mathematical logic as based on the theory of types
  12. Horsten, Leon. Philosophy of Mathematics (англ.). — Stanford Encyclopedia of Philosophy. Дата обращения: 15 ноября 2017. Архивировано 11 марта 2018 года.

Литература
  • Гильберт Д., Аккерман В. Основы теоретической логики. М., 1947.
  • Гришин В. Н. Непредикативное определение // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
  • Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — 446 с.
  • Непредикативное определение // Философский энциклопедический словарь. — М.: Советская энциклопедия, 1983. — 840 с.
  • Френкель Α.- Α., Баρ-Xиллел И. Основания теории множеств. М., 1966.
  • Чёрч Α. Введение в математическую логику. М., 1960.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.