Модель Ходжкина — Хаксли
Модель Ходжкина — Хаксли — математическая модель, описывающая генерацию и распространение потенциалов действия в нейронах. Подобные модели были созданы впоследствии и для других электрически возбуждаемых клеток — например, для сердечных миоцитов; все модели такого рода описывают автоволновые процессы в активных средах. Точечная модель Ходжкина — Хаксли представляет собой систему обыкновенных дифференциальных уравнений, которая, в частности, пригодна и для описания характеристик электрического сигнала.
Модель была разработана Аланом Ллойдом Ходжкином и Эндрю Хаксли в 1952 году для описания электрических механизмов, которые обусловливают генерацию и передачу нервного сигнала в гигантском аксоне кальмара[1]. За это авторы модели получили Нобелевскую премию в области физиологии и медицины за 1963 год.
Основные компоненты
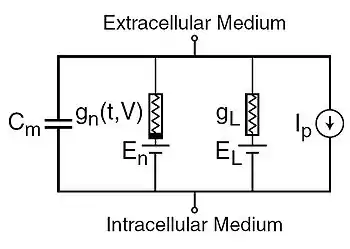
Компоненты электрической схемы, что соответствует модели Ходжкина — Хаксли, изображены на рисунке. В данной схеме каждый компонент возбуждаемой клетки имеет свой биофизический аналог. Внутреннему липидному слою клеточной мембраны соответствует электроёмкость (). Потенциал-зависимые ионные каналы отвечают за нелинейную электрическую проводимость (, где — отдельный вид ионных каналов) — это означает, что проводимость является потенциал-время-зависимой величиной. Эта составляющая системы, как было показано исследователями позже, реализуется благодаря белковым молекулам, которые образуют потенциал-зависимые ионные каналы, каждый из которых отмечен некоторой вероятностью открытия, величина которой зависит от электрического потенциала (или электрического напряжения) мембраны клетки. Каналы мембранных пор отвечают за пассивную проводимость (, где индекс означает англ. leak — «течь, утечка»). Электрохимический градиент побуждает ионы к движению через мембранные каналы, он показан с помощью источников напряжения с соответствующей электродвижущей силой ( и ), величина которой определяется реверсивным потенциалом для соответствующего вида иона. Ионные транспортёры соответствуют источникам тока ().
Производная по времени от мембранного потенциала клеточной мембраны () при описанных условиях пропорциональна сумме токов в полной электрической цепи. Она описывается следующим уравнением:
где означает величину электрического тока, генерируемого отдельным видом ионов.
Характеристики ионного тока
Электрический ток, проходящий через ионные каналы, может быть математически выражен следующим уравнением:
где — равновесный потенциал -го ионного канала. В случае потенциал-зависимых ионных каналов канальная проводимость является функцией времени и потенциала (электрического напряжения) — на рисунке, в то время как пассивная проводимость является величиной постоянной ( на рисунке). Ток, генерируемый ионными транспортерами, зависит от вида ионов, который переносит соответствующий транспортёр. Ниже приведено более подробное описание перечисленных величин.
Потенциал-зависимые ионные каналы
В терминах модели Ходжкина — Хаксли , проводимость потенциал-зависимых каналов, описывается следующим образом:
где и являются константами скорости реакций закрытия и открытия каналов, соответственно. Они численно равны доле от максимально возможной проводимости через данный вид каналов в каждый момент времени при каждой величине мембранного потенциала. является максимальным возможным значением проводимости. и — константы, и — временны́е константы процессов активации и деактивации каналов, соответственно. и является стабилизированными значениями и при величине времени, стремящейся к бесконечности, и обычно рассчитываются из уравнения Больцмана как функции .
Для характеристики ионных каналов, последние два уравнения модифицируются для условий, когда на мембране поддерживается постоянная величина электрического потенциала — модификация уравнений Ходжкина — Хаксли, сделанная Марквардтом[2] . Когда мембранный электрический потенциал поддерживается на постоянном уровне (англ. voltage-clamp), для каждого значения этого потенциала нелинейные уравнения, описывающие пропуск ионов через каналы, редуцируются к линейным дифференциальным уравнениям следующего вида:
Таким образом, для каждого значения мембранного потенциала , величина электрического тока описывается следующим уравнением:
Для аппроксимации кривых, которые генерируют данные уравнения, до значений клеточных токов при фиксированном значении мембранного потенциала используется алгоритм Левенберга — Марквардта[3][4].
Пассивные каналы
Пассивные каналы отвечают за проницаемость мембраны для ионов в спокойном состоянии (не во время проведения потенциала действия), и ток через них описывается теми же уравнениями, что и для потенциал-зависимых каналов, но при условии постоянной величины проводимости ().
Ионные транспортёры
Мембранный электрический потенциал генерируется с помощью поддержания концентрационных градиентов ионов, присутствующих в физиологических жидкостях организма, относительно клеточной мембраны. Наиболее важными из белков-транспортёров, которые поддерживают мембранный потенциал, является натриево-кальциевый (транспортирует один ион Са2+ внутрь клетки в обмен на три иона Na+, транспортируемых наружу), натриево-калиевый (транспортирует один ион Na+ наружу в обмен на один ион К+ внутрь) и хлорный (транспортирует из клетки наружу ионы Cl−)[5][6].
Модификации и альтернативные модели
Модель Ходжкина — Хаксли является одним из важнейших достижений в биофизике и нейрофизиологии XX века. Со временем она была модифицирована в следующих направлениях:
- Основываясь на экспериментальных данных, в неё были инкорпорированы дополнительные виды ионных каналов и транспортёров.
- Основываясь на данных микроскопии высокого разрешения, в уравнение добавлены элементы, характеризующие сложную морфологию отростков нервных клеток (аксонов и дендритов).
Также на общих принципах модели Ходжкина — Хаксли были разработаны несколько моделей, описывающих взаимную активацию и деактивацию в нейронных сетях, а также молекулярную динамику генерации потенциала действия.
См. также
Литература
- Hodgkin, A., and Huxley, A. (1952): A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117:500—544.
- Marquardt, D. (1963): An algorithm for the least-squares estimation of nonlinear parameters. SIAM J. Appl. Math. 11 (2):431—441.
- Levenberg, K. (1944): A method for the solution of certain non-linear problems in least-squares. Q. Appl. Math. 2 (2):164—168.
- Johnston, D., and Wu, S. (1997): Foundations of Cellular Neurophysiology, chapter 6. MIT Press, Cambridge, MA. — ISBN 0-262-10053-3.
- Hille, B. (2001): Ionic Channels of Excitable Membranes. — (3rd ed.). — Sinauer Associates, Inc., Sunderland, MA. — ISBN 0-87893-321-2
- Encyclopedia of Neuroscience. — 3rd edition. — Elsevier Science, 2004. — ISBN 0-444-51432-5
Ссылки
- Интерактивный Java-апплет модели Ходжкина — Хаксли. Параметры модели и параметры возбуждения могут меняться; возможно построение диаграмм изменения значений переменных.
- Интерактивный Java-апплет уравнений Ходжкина — Хаксли для численного решения дифференциальных уравнений Ходжкина — Хаксли.
- Статья Ходжкина и Хаксли с описанием модели генерации потенциала действия. Часть первая: Сurrents carried BY Sodium AND Potassium ions Through The Membrane Of The Giant AXON Of Loligo.
- Статья Ходжкина и Хаксли с описанием модели генерации потенциала действия. Часть вторая: The Components Of Membrane conductance In The Giant Axon Of Loligo.
- Статья Ходжкина и Хаксли с описанием модели генерации потенциала действия. Часть третья: The Dual Effect Of Membrane Potential On Sodium conductance In The Giant Axon Of Loligo.
- Статья Ходжкина и Хаксли с описанием модели генерации потенциала действия. Часть четвёртая: A quantitative description of membrane current and its application to conduction and excitation in nerve.
- Neural Impulses: The Action Potential In Action. by Garrett Neske, The Wolfram Demonstrations Project.