Логический квадрат
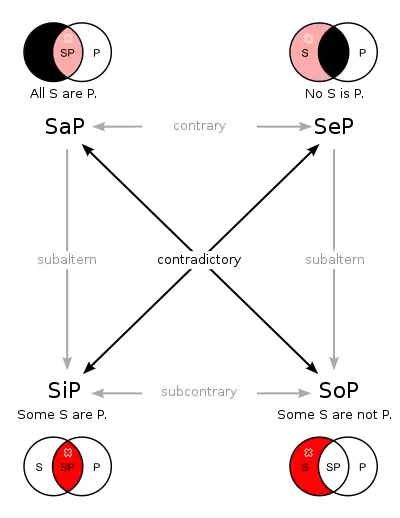
Логический квадрат, или квадрат оппозиции — это диаграмма, представляющая отношения между основными категориальными пропозициями, которые, в свою очередь, утверждают, что все или некоторые из членов одной категории (субъектный термин) включены в другую (предикатный термин).

Происхождение квадрата может быть приписано Аристотелю, который впервые провел различие между двумя оппозициями: противоречие и противоположность. Но Аристотель не делал каких-либо схем. Теория была разработана спустя несколько веков Боэцием и Абеляром. Автором современного логического квадрата является византийский учёный Михаил Пселл[1][2].
Концепцию логического квадрата разрабатывали такие философы и логики, как Уильям из Шервуда, Роджер Бэкон, Жан Буридан, Питер Стросон.[3]
Содержание
В традиционной логике пропозиция (лат. Propositio) — это устное утверждение (oratio enunciativa), а не значение утверждения, как в современной философии языка и логики. Категорическое предложение — это простое предложение, содержащее два термина, субъект (S) и предикат (P), в котором предикат либо утверждается, либо отрицается в отношении субъекта.
Каждая категориальная пропозиция может быть сведена к одной из четырех логических форм, названных A, E, I и O на основе латинского алфавита - лат. affirmo (подтверждаю) для утвердительных пропозиций A и I и лат. nego (отрицаю) для отрицательных пропозиций E и O.
- Пропозиция «A», универсальное утвердительное (universalis affirmativa), форма которого на латыни - «omne S est P», обычно переводится как «каждый S является P».
- Пропозиция «E», универсальное отрицание (universalis negativa), на латинском «nullum S est P», обычно переводится как «ни один S являются P».
- Пропозиция «I», частное утвердительное (specificis affirmativa), на латинском «quoddam S est P», обычно переводится как «некоторые S являются P».
- Пропозиция «O», частное отрицание (specificis negativa), на латинском «quoddam S nōn est P», обычно переводится как «некоторые S не являются P».
В форме таблицы:
| Название | Символ | Латинский | Русский* | Мнемоническая часть | Современная форма[4] |
|---|---|---|---|---|---|
| Универсальное утвердительное | A | Omne S est P. | Каждый S является P. (S всегда P.) | лат. affirmo (подтверждаю) | |
| Универсальное отрицание | E | Nullum S est P. | Ни один S являются P. (S никогда P.) | лат. nego (отрицаю) | |
| Частное утвердительное | I | Quoddam S est P. | Некоторые S являются P. (S иногда P.) | лат. affirmo (подтверждаю) | |
| Частное отрицание | O | Quoddam S nōn est P. | Некоторые S не являются P. (S не всегда P.) | лат. nego (отрицаю) |
* Утверждение «А» можно сформулировать как «Все S есть P.» Однако предложение «E», когда оно формулируется соответственно как «Все S не является P.» является неоднозначным[5], потому что это может быть пропозиция E или O, поэтому для определения формы требуется контекст; стандартная форма «Ни один S являются P» однозначна, поэтому она предпочтительна. Пропозиция «O» также принимает форму «Некоторые S не являются P» и «Некоторый S не является P.» (буквально латинское Quoddam S nōn est P.)
Аристотель утверждает (в шестой и седьмой главах «Об истолковании» (лат. De Interpretatione, др.-греч. Περὶ Ἑρμηνείας)) что между четырьмя типами пропозиций существуют определенные логические отношения. Он говорит, что каждой пропозиции соответствует в точности одно отрицание и что каждая пропозиция и её отрицание «противоположны», так что всегда одна из них должна быть истинной, а другая ложной. Пару утвердительных и отрицательных пропозиций он называет «противоречием» (лат. contradictio). Примеры противоречий: «каждый человек белый» и «не каждый человек белый» (также читается как «некоторые люди не белые»), «ни один человек не белый» и «какой-то человек белый».
«Противоположные» (лат. contrariae) пропозиции таковы, что оба не могут быть правдой одновременно. Примерами этого являются универсальное утвердительное «каждый человек белый» и универсальное отрицательное «ни один человек не белый». Это не может быть правдой одновременно. Однако это не противоречие, потому что оба они могут быть ложными. Например, неверно, что каждый мужчина белый, поскольку некоторые мужчины не белые. Однако неверно также, что нет белых людей, поскольку есть некоторые белые люди.
Поскольку каждая пропозиция имеет противоречивую противоположность и поскольку противоречие истинно, когда противоположное ложно, из этого следует, что противоположности противоположностей (лат. subcontrariae) могут быть истинными, но не могут быть ложными. Поскольку субпротиворечия являются отрицанием универсальных утверждений, средневековые логики называли их «частными» утверждениями.
Другая логическая оппозиция, подразумеваемая этим, хотя и не упомянутая прямо Аристотелем, — это «альтерация» (лат. alternatio — изменение), состоящее из «субальтерация» и «суперальтерация». Альтерация — это отношение между конкретной пропозицией и универсальной пропозицией того же качества, при котором одно подразумевается другим. Частное является субальтерацией по отношению к универсальному, которое является суперальтерацией частного. Например, если «каждый человек белый» верно, то противоположное «ни один человек не белый» — ложно. Следовательно, противоречивое утверждение «какой-то мужчина белый» верно. Точно так же универсальное «ни один человек не белый» подразумевает конкретное «не каждый человек белый»[6][7].
В итоге:
- Универсальные пропозиции противоречат друг другу: «каждый человек справедлив» и «никто несправедлив» не могут быть истинными вместе, хотя одно может быть истинным, а другое ложным, а также оба могут быть ложными (если хотя бы один человек справедлив, и хотя бы один человек несправедлив).
- Частные утверждения являются субпротиворечием. «Кто-то справедливый» и «какой-то мужчина несправедливый» не могут быть ложными вместе.
- Конкретная пропозиция одного качества является субальтерацией универсального утверждения того же качества, которое является суперальтерацией конкретного пропозиции, потому что в аристотелевской семантике «каждый A есть B» подразумевает «некоторое A является B» и «никакое A не является B». подразумевает, что «некоторый A не является B». Стоит обратить внимание, что современные формальные интерпретации предложений интерпретируют «каждый A является B» как «для любого x, x является A подразумевает, что x является B», что не означает, что «некоторый x является A». Однако это вопрос семантической интерпретации и не означает, как иногда утверждают, что аристотелевская логика «ошибочна».
- Универсальное утвердительное и частное отрицательное противоречат друг другу. Если какой-то A не является B, не каждый A является B. И наоборот, хотя это не так в современной семантике; считалось, что если каждый A не является B, то какой-то A не является B. Эта интерпретация вызвала трудности (см. ниже). В то время как греческий язык Аристотеля представляет конкретный отрицание не как «некоторые A не B», а как «не все A есть B», автор в своем комментарии к Об истолковании переводит этот конкретный негатив как «quoddam A nōn est B», буквально «определенное А не является В», и во всех средневековых трудах по логике принято представлять конкретное суждение таким образом.
Эти отношения стали основой диаграммы, созданной Боэцием и использовавшейся средневековыми логиками для классификации логических отношений. Предложения помещены в четыре угла квадрата, а отношения представлены в виде линий, проведенных между ними, отсюда и происходит название «логический квадрат».
Проблема экзистенциального значения
Субпротиворечия, которые средневековые логики представляли в форме 'quoddam A est B' (некоторая конкретная A является B) и 'quoddam A non est B' (некоторая конкретная A не является B) не могут быть ложными, поскольку их универсальных противоречивые утверждения (каждое A является B/не A является B) одновременно не могут быть правдой. Это приводит к затруднению, которое впервые было обнаружено Пьером Абеляром. «Некоторый A является B», кажется, подразумевает «что-то является A». Например, «какой-то человек белый», кажется, подразумевает, что по крайней мере что-то одно является человеком, а именно человек, который должен быть белым, если «какой-то человек белый» верно. Но «какой-то человек не белый» также подразумевает, что что-то является человеком, а именно человеком, который не белый, если утверждение «какой-то человек не белый» верно. Но аристотелевская логика требует, чтобы одно из этих утверждений обязательно было истинным. Оба не могут быть ложными. Следовательно (поскольку оба подразумевают, что что-то является человеком), следует, что обязательно что-то есть человек, т.е. люди существуют. Но (как указывает Абеляр в «Диалектике») неужели люди могут не существовать[8]?
Для того, чтобы безусловно было ни одного человека, ни утверждение «каждый человек есть человек» не истинно, ни «некоторый человек не является человеком».
Оригинальный текст (англ.)[показатьскрыть]For with absolutely no man existing, neither the proposition 'every man is a man' is true nor 'some man is not a man'.
Абеляр также указывает, что субпротиворечивые слова, содержащие субъектные термины, ничего не обозначающие, такие как «человек, который есть камень», являются ложными.
Если «каждый каменный человек - камень» верно, то верно и его преобразование «per accidens» («некоторые камни - каменные люди»). Но никакой камень не является каменным человеком, потому что ни этот человек, ни тот человек и т.д. не являются камнем. Но также и то, что «некий каменный человек - не камень» ложно по необходимости, поскольку невозможно предположить, что это правда.
Оригинальный текст (англ.)[показатьскрыть]If 'every stone-man is a stone' is true, also its conversion per accidens is true ('some stones are stone-men'). But no stone is a stone-man, because neither this man nor that man etc. is a stone. But also this 'a certain stone-man is not a stone' is false by necessity, since it is impossible to suppose it is true.
Теренс Парсонс утверждает, что древние философы не испытывали проблемы экзистенциального значения, поскольку только формы A и I имели экзистенциальное значение.
Утверждения имеют экзистенциальное значение, а отрицательные - нет. Таким образом, древние не видели несогласованности квадрата, сформулированной Аристотелем, потому что не было непоследовательности, которую можно было бы увидеть.
Оригинальный текст (англ.)[показатьскрыть]Affirmatives have existential import, and negatives do not. The ancients thus did not see the incoherence of the square as formulated by Aristotle because there was no incoherence to see.
Далее он цитирует средневекового философа Вильгельма из Мёрбеке:
В утвердительных предложениях термин всегда используется для предположения чего-либо. Таким образом, если оно ни о чем не предполагает, это утверждение ложно. Однако в отрицательных суждениях утверждается либо то, что термин не предполагает чего-либо, либо что он предполагает что-то, предикат чего действительно отрицается. Таким образом, отрицательное суждение имеет две причины истинности.
Оригинальный текст (англ.)[показатьскрыть]In affirmative propositions a term is always asserted to supposit for something. Thus, if it supposits for nothing the proposition is false. However, in negative propositions the assertion is either that the term does not supposit for something or that it supposits for something of which the predicate is truly denied. Thus a negative proposition has two causes of truth.
И указывает на перевод Аристотеля Боэция как на порождение ошибочного представления о том, что форма O имеет экзистенциальное значение.
Но когда Боэций комментирует этот текст, он иллюстрирует доктрину Аристотеля известной ныне диаграммой и использует формулировку «Некоторые люди не справедливы». Так что это должно было показаться ему естественным эквивалентом на латыни. Нам это кажется странным по-английски, но его это не беспокоило.
Оригинальный текст (англ.)[показатьскрыть]But when Boethius comments on this text he illustrates Aristotle's doctrine with the now-famous diagram, and he uses the wording 'Some man is not just'. So this must have seemed to him to be a natural equivalent in Latin. It looks odd to us in English, but he wasn't bothered by it.
Современные логические квадраты
В 19 веке Джордж Буль выступал за требование экзистенциального значения обоих терминов в конкретных утверждениях (I и O), но допускал, чтобы все термины универсальных утверждений (A и E) не имели экзистенциального значения. Это решение сделало диаграмму Венна особенно простой в использовании для терминологической логики. Логические квадрат при булевом наборе допущений часто называют современным логическим квадратом. В современном квадрате оппозиции утверждения A и O противоречат друг другу, как и E и I, но все другие формы оппозиции перестают существовать; нет никаких противоречий, субпротиворечия или субальтерации. Таким образом, с современной точки зрения, часто имеет смысл говорить о «противоположности» утверждения, вместо того, чтобы настаивать, как это делали более старые логики, на том, что у утверждения есть несколько различных противоположностей, которые находятся в разных видах противоположностей с утверждением.
Begriffsschrift Готлоба Фреге также представляет собой логический квадрат, почти идентичен классическому квадрату, показывая противоречия, субальтерации и противоположности между четырьмя формулами, построенными на основе универсальной квантификации, отрицания и импликации.
Семиотический квадрат Альгирдаса Жюльена Греймаса был получен из работ Аристотеля.
Традиционный логический квадрат теперь часто сравнивают с квадратами, основанными на внутреннем и внешнем отрицании[14].
Логические шестиугольники и другие би-симплексы
Логический квадрат был расширен до логического шестиугольника, который включает отношения шести утверждений. Был независимо открыт Augustin Sesmat и Robert Blanché[15]. Было доказано, что и квадрат, и шестиугольник, за которым следует «логический куб», принадлежат к регулярной серии n-мерных объектов, называемых «логическими би-симплексами размерности n».
См. также
Примечания
- Логический квадрат // Философская Энциклопедия. В 5-х т. — М.: Советская энциклопедия. Под редакцией Ф. В. Константинова. 1960—1970.
- Логический квадрат // Словарь по логике. — М.: Туманит, изд. центр ВЛАДОС. А.А.Ивин, А.Л.Никифоров. 1997.
- The Traditional Square of Opposition в Стэнфордской энциклопедии философии
- The Traditional Square of Opposition: 1.1 The Modern Revision of the Square в Стэнфордской энциклопедии философии
- Kelley, David. The Art of Reasoning: An Introduction to Logic and Critical Thinking. — 4. — New York, NY : W.W. Norton & Company, Inc., 2014. — P. 150. — ISBN 978-0-393-93078-8.
- Parry & Hacker, Aristotelian Logic (SUNY Press, 1990), p. 158.
- Cohen & Nagel, Introduction to Logic Second Edition (Hackett Publishing, 1993), p. 55.
- В его работе Диалектика
- Re enim hominis prorsus non existente neque ea vera est quae ait: omnis homo est homo, nec ea quae proponit: quidam homo non est homo
- Si enim vera est: Omnis homo qui lapis est, est lapis, et eius conversa per accidens vera est: Quidam lapis est homo qui est lapis. Sed nullus lapis est homo qui est lapis, quia neque hic neque ille etc. Sed et illam: Quidam homo qui est lapis, non est lapis, falsam esse necesse est, cum impossibile ponat
- The Traditional Square of Opposition в Стэнфордской энциклопедии философии
- (SL I.72) Loux 1974, 206
- The Traditional Square of Opposition
- Westerståhl, 'Classical vs. modern squares of opposition, and beyond', in Beziau and Payette (eds.), The Square of Opposition: A General Framework for Cognition, Peter Lang, Bern, 195-229.
- N-Opposition Theory Logical hexagon
Литература
- Челпанов Г. Учебник логики. — 9-е издание. — М., 1998.
- Гетманова А. Д. Логика. — Книжный дом «Университет», 1998. — 480 с.