Коника девяти точек
Коника девяти точек полного четырёхугольника — это коническое сечение, проходящее через три диагональные точки и шесть середин сторон полного четырёхугольника.
Коническое сечение девяти точек описал Максим Бохер в 1892 году. Более известная окружность девяти точек является частным случаем коники Бохера. Другой частный случай — гипербола девяти точек.
Определение
Бохер использовал четыре точки полного четырёхугольника как три вершины треугольника и одну независимую точку:
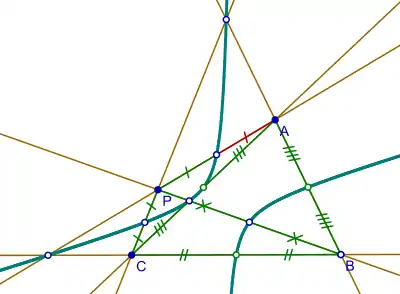
- Пусть задан треугольник ABC и точка P на плоскости. Коническое сечение можно провести через следующие девять точек:
- середины сторон треугольника ABC,
- середины отрезков, соединяющих P с вершинами треугольника,
- точки, где эти прямые, проходящие через P и вершины треугольника, пересекают стороны треугольника.
Свойства
Коническое сечение будет эллипсом, если P лежит внутри треугольника ABC или в одной из областей плоскости, отделённых от внутренности треугольника двумя сторонами. В противном случае коника будет гиперболой. Бохер заметил, что в случае, когда P является ортоцентром, получим окружность девяти точек, а когда P является центром описанной окружности треугольника ABC, коника будет равнобочной гиперболой.
В 1912 году Мод Минторн показал, что коника девяти точек является геометрическим местом центров конических сечений, проходящих через четыре заданные точки.
Литература
- Maxime Bôcher. Nine-point Conic // Annals of Mathematics. — 1892. — Т. 6, вып. 5. — С. 132.
- Fanny Gates. Some Considerations on the Nine-point Conic and its Reciprocal // Annals of Mathematics. — 1894. — Т. 8, вып. 6. — С. 185–8.
- Maud A. Minthorn. The Nine Point Conic. — Master's dissertation at University of California, Berkeley, 1912.
- Eric W. Weisstein. Nine-point conic. MathWorld.
- Michael DeVilliers. The nine-point conic: a rediscovery and proof by computer // International Journal of Mathematical Education in Science and Technology. — Taylor & Francis, 2006. — Т. 37, вып. 1.
- Christopher Bradley. The Nine-point Conic and a Pair of Parallel Lines. — University of Bath.
Литература для дальнейшего чтения
- W. G. Fraser. On relations of certain conics to a triangle // Proceedings of the Edinburgh Mathematical Society. — 1906. — Т. 25. — С. 38–41.
- Thomas F. Hogate. On the Cone of Second Order which is Analogous to the Nine-point Conic // Annals of Mathematics. — 1894. — Т. 7. — С. 73–6.
- P. Pinkerton. On a nine-point conic, etc. // Proceedings of the Edinburgh Mathematical Society. — 1905. — Т. 24. — С. 31–3.