Когомологии Александрова — Чеха

Пусть ${\displaystyle X}$ — топологическое пространство, ${\displaystyle {\mathcal {V}}}$ — открытое покрытие ${\displaystyle X}$. Обозначим через ${\displaystyle N_{\mathcal {V}}}$ нерв покрытия ${\displaystyle {\mathcal {V}}}$.

Предположим, покрытие ${\displaystyle {\mathcal {W}}}$ вписано в покрытие ${\displaystyle {\mathcal {V}}}$, то есть любое множество из ${\displaystyle {\mathcal {W}}}$ содержится в некотором множестве из ${\displaystyle {\mathcal {V}}}$. Выберем отображение, сопоставляющее каждому множеству из ${\displaystyle {\mathcal {W}}}$ содержащее его множество из ${\displaystyle {\mathcal {V}}}$. Это отображение индуцирует отображение нервов ${\displaystyle f\colon N_{\mathcal {W}}\to N_{\mathcal {V}}}$. Индуцированный гомоморфизм колец когомологий ${\displaystyle f^{*}\colon H^{*}(N_{\mathcal {V}},G)\to H^{*}(N_{\mathcal {W}},G)}$ не зависит от выбора ${\displaystyle f}$. (Поскольку мы работаем с симплициальными комплексами, неважно, какую из теорий когомологий мы выбираем.)

Кольца когомологий ${\displaystyle H^{*}(N_{\mathcal {V}},G)}$ с гомоморфизмами ${\displaystyle f^{*}}$ образуют обратную систему. Это даёт возможность перейти к обратному пределу

${\displaystyle {\check {H}}^{*}(X,G)=\varprojlim H^{*}(N_{\mathcal {V}},G).}$

Полученное кольцо ${\displaystyle {\check {H}}^{*}(X,G)}$ называется когомологиями Чеха пространства ${\displaystyle X}$ с коэффициентами в ${\displaystyle G}$.

Польская окружность

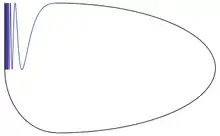
• Для патологических пространств когомологии Чеха могут отличатся от сингулярных когомологий.
  • Например, если X — польская окружность, то ${\displaystyle {\check {H}}^{1}(X;\mathbb {Z} )=\mathbb {Z} }$, тогда как ${\displaystyle H^{1}(X;\mathbb {Z} )=0.}$
• Если X гомотопически эквивалентен СW-комплексу, то когомологии Чеха ${\displaystyle {\check {H}}^{*}(X;A)}$ естественно изоморфны сингулярным когомологиям ${\displaystyle H^{*}(X;A)}$.
• Если X является гладким многообразием, то когомологии Чеха ${\displaystyle {\check {H}}^{*}(X;\mathbb {R} )}$ естественно изоморфны когомологиям де Рама.

• Когомологии Чеха с коэффициентами в пучке

• Александров П. С., "Аnn. of Math. ", 1928, v. 30, p. 101-87;
• Сесh Е., "Fundam. math. ", 1932, t. 19, p. 149-83;
• Bott, Raoul; Loring Tu. Differential Forms in Algebraic Topology (неопр.). — New York: Springer, 1982. — ISBN 0-387-90613-4.
• Hatcher, Allen Algebraic Topology (неопр.). — Cambridge University Press, 2002. — ISBN 0-521-79540-0.
• Wells, Raymond Differential Analysis on Complex Manifolds (англ.). — Springer-Verlag, 1980. — ISBN 0-387-90419-0. Chapter 2 Appendix A