Квантовая теория рассеяния

Квантовая теория рассеяния — раздел квантовой механики, описывающий рассеяние частиц на изолированном рассеивающем центре. В простейшем случае, этот центр характеризуется потенциалом. Обычно предполагается, что потенциал стремится к нулю по мере удаления от рассеивающего центра.

Постановка задачи

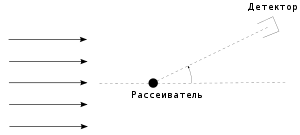
Постановка задачи о квантовом рассеянии

В учебнике Ландау и Лифшица по квантовой механике [1] задача о рассеянии ставится следующим образом.

На силовой центр падает пучок частиц с волновым вектором ${\vec {k}}_{0}$ и плотностью N. Измеряется число частиц dN, которые попадают в детектор в единицу времени:

dN=q(\theta ,\phi )Nd\Omega

где $\theta$ и $\phi$ сферические углы детектора в системе координат, начало которой помещено в рассеивающий центр (ось z направлена вдоль вектора ${\vec {k}}_{0}$ , а $d\Omega$ -- телесный угол, под которым детектор виден из начала координат. Для решения этой задачи рассмотрим стационарное уравнение Шредингера:

\left(-{\frac {\hbar ^{2}}{2m_{0}}}\Delta +V(r)\right)\psi ({\vec {r}})=E\psi ({\vec {r}})

Свободная частица, движущаяся в положительном направлении оси z, описывается плоской волной: $\psi ({\vec {r}})=exp(i{\vec {k}}_{0}\cdot {\vec {r}})$ . Рассеянные частицы описываются вдали от центра расходящейся сферической волной вида: $A(\theta ,\phi ){\frac {exp(ik_{0}r)}{r}}$ , следовательно, будем искать решение уравнения Шредингера со следующей асимптотикой на бесконечности:

\psi ({\vec {r}})\approx exp(i{\vec {k}}_{0}\cdot {\vec {r}})+A(\theta ,\phi ){\frac {exp(ik_{0}r)}{r}}

В результате решения этого уравнения мы получим амплитуду рассеяния: $A(\theta ,\phi )$ и, следовательно, эффективное сечение рассеяния: $d\sigma =|A(\theta ,\phi )|^{2}d\Omega$ При решении задач рассеяния в квантовой механике широко применяется метод фазовых функций.

Классическое и квантовое рассеяние

Вышеприведенная постановка задачи существенно отличается от классической теории рассеяния, где начальное условие характеризуется прицельным параметром. В квантовой механике понятие траектории теряет смысл, поэтому говорить о прицельном параметре некорректно.

Возможна формулировка задачи о рассеянии, которая допускает единую интерпретацию как в классической, так и в квантовой механике [2]

Примечания

Ландау Л.Д., Лифшиц Е.М. Квантовая механика (неопр.). — 1989.
Ю.М.Широков. Единый формализм для квантовой и классической теорий рассеяния (рус.) // Теоретическая и математическая физика : журнал. — 1979. — Т. 38, № 3. — С. 313—319.

Литература

Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5.
С. Сунакава Квантовая теория рассеяния. - М., Мир, 1979. - 265 c.
Базь А. И., Зельдович Я. Б., Переломов А. М. Рассеяние, реакции и распады в нерелявиcтской квантовой механике. - М., Наука, 1966.
Ву Т. Ю., Омура Т. Квантовая теория рассеяния. - М., Наука, 1969.
Гольдбергер М., Ватсон К. Теория столкновений. - М., Мир, 1967.
Мотт Н., Месси Г. Теория атомных столкновений. - М., Мир, 1969.
Ньютон Р. Теория рассеяния волн и частиц. - М., Мир, 1969.
Мигдал А. Б., Крайнов В. П. Приближенные методы квантовой механики. - М., Наука, 1966.
Жигунов, В. П., Захарьев, Б. Н. Методы сильной связи каналов в квантовой теории рассеяния. - М., Атомиздат, 1974. - 223 с.
Де Альфаро, В., Редже, Т. Потенциальное рассеяние. - М., Мир, 1966. - 274 с.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Ландау Л.Д., Лифшиц Е.М. Квантовая механика (неопр.). — 1989.

[2] Ю.М.Широков. Единый формализм для квантовой и классической теорий рассеяния (рус.) // Теоретическая и математическая физика : журнал. — 1979. — Т. 38, № 3. — С. 313—319.