Канторова лестница
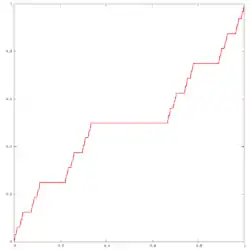
Канторова лестница — пример непрерывной монотонной функции , которая не является константой, но при этом имеет производную, равную нулю в почти всех точках (сингулярной функции). Иногда называется «Чёртовой лестницей» или «дьявольской лестницей».[1]
Построения
Стандартное
В точках 0 и 1 значение функции принимается равным соответственно 0 и 1. Далее интервал (0, 1) разбивается на три равные части , и . На среднем сегменте полагаем . Оставшиеся два сегмента снова разбиваются на три равные части каждый, и на средних сегментах полагается равной и . Каждый из оставшихся сегментов снова делится на три части, и на внутренних сегментах определяется как постоянная, равная среднему арифметическому между соседними, уже определенными значениями . На остальных точках единичного отрезка определяется по непрерывности. Полученная функция называется канторовой лестницей.
По двоичной и троичной записи
Любое число можно представить в троичной системе счисления , . Если в записи встречается 1, выбросим из неё все последующие цифры и в оставшейся последовательности заменим каждую двойку на 1. Получившаяся последовательность даёт запись значения канторовой лестницы в точке в двоичной системе счисления.
Свойства
- Производная канторовой лестницы определена и равна нулю во всех точках, кроме канторова множества.
- Канторова лестница непрерывна, ограниченной вариации, но не абсолютно непрерывна.
- Канторова лестница не обладает свойством Лузина.
См. также
Ссылки
- Weisstein, Eric W. Devil's Staircase (англ.) на сайте Wolfram MathWorld.