Интегралы Френеля

Нормализованные интегралы Френеля, S(x) и C(x). На этих кривых аргумент подынтегральных тригонометрических функций равен ${\displaystyle \pi t^{2}/2}$, а не ${\displaystyle t^{2}}$, как на рисунке выше.

Интегралы Френеля могут быть представлены степенными рядами, сходящимися при всех x:

${\displaystyle S(x)=\int \limits _{0}^{x}\sin(t^{2})\,dt=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{4n+3}}{(4n+3)(2n+1)!}}={\frac {x^{3}}{3}}-{\frac {x^{7}}{42}}+{\frac {x^{11}}{1320}}-\cdots ,}$

${\displaystyle C(x)=\int \limits _{0}^{x}\cos(t^{2})\,dt=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{4n+1}}{(4n+1)(2n)!}}=x-{\frac {x^{5}}{10}}+{\frac {x^{9}}{216}}-\cdots .}$

Некоторые авторы[1] используют в качестве аргумента тригонометрических подынтегральных функций ${\displaystyle {\frac {\pi }{2}}t^{2}}$. Таким образом определенные интегралы Френеля получаются из определённых выше интегралов заменой переменной ${\displaystyle t\to {\sqrt {\frac {\pi }{2}}}t}$ и умножением интегралов на ${\displaystyle {\sqrt {\frac {2}{\pi }}}}$.

Спираль Корню (x,y)=(C(t), S(t)). Спираль стремится к центрам отверстий при ${\displaystyle t\rightarrow \pm \infty }$.

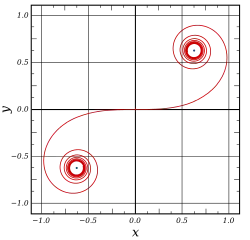
Спираль Корню, также известная как клотоида, — это кривая, являющаяся параметрическим графиком S(t) от C(t). Спираль Корню была придумана Мари Альфредом Корню для облегчения расчёта дифракции в прикладных задачах.

Так как

${\displaystyle C\,'(t)^{2}+S\,'(t)^{2}=\sin ^{2}(t^{2})+\cos ^{2}(t^{2})=1,}$

то в такой параметризации касательный вектор имеет единичную длину, так что t является длиной кривой, измеряемой от точки (0,0). Следовательно, обе ветви спирали имеют бесконечную длину.

Кривизна этой кривой в любой точке пропорциональна длине дуги, заключённой между этой точкой и началом координат. Благодаря этому свойству она применяется в строительстве дорог, так как угловое ускорение машины, движущейся по этой кривой с постоянной скоростью, будет оставаться постоянным.

• ${\displaystyle S(x)}$ и ${\displaystyle C(x)}$ — нечётные функции ${\displaystyle x}$.

• Асимптотики интегралов Френеля при ${\displaystyle x\to \infty }$ даются формулами

${\displaystyle S(x)={\sqrt {\frac {\pi }{2}}}\left({\frac {{\mbox{sign}}{(x)}}{2}}-{\frac {\cos {(x^{2})}}{x{\sqrt {2\pi }}}}\left[1+O(x^{-4})\right]-{\frac {\sin {(x^{2})}}{x^{3}{\sqrt {8\pi }}}}\left[1+O(x^{-4})\right]\right),}$

${\displaystyle C(x)={\sqrt {\frac {\pi }{2}}}\left({\frac {{\mbox{sign}}{(x)}}{2}}+{\frac {\sin {(x^{2})}}{x{\sqrt {2\pi }}}}\left[1+O(x^{-4})\right]-{\frac {\cos {(x^{2})}}{x^{3}{\sqrt {8\pi }}}}\left[1+O(x^{-4})\right]\right).}$

• Используя разложение в ряд, можно построить аналитическое продолжение интегралов Френеля на всю комплексную плоскость. Комплексные интегралы Френеля выражаются через функцию ошибок как

${\displaystyle S(x)={\frac {\sqrt {\pi }}{4}}\left({\sqrt {i}}\,\mathrm {erf} ({\sqrt {i}}\,x)+{\sqrt {-i}}\,\mathrm {erf} ({\sqrt {-i}}\,x)\right)}$

${\displaystyle C(x)={\frac {\sqrt {\pi }}{4}}\left({\sqrt {-i}}\,\mathrm {erf} ({\sqrt {i}}\,x)+{\sqrt {i}}\,\mathrm {erf} ({\sqrt {-i}}\,x)\right)}$.

• Интегралы Френеля не выражаются через элементарные функции, кроме частных случаев. Предел этих функций при ${\displaystyle x\rightarrow \infty }$ равен

${\displaystyle \int \limits _{0}^{\infty }\cos t^{2}\,dt=\int \limits _{0}^{\infty }\sin t^{2}\,dt={\frac {\sqrt {2\pi }}{4}}={\sqrt {\frac {\pi }{8}}}.}$

Вычисление

Контур, используемый для вычисления предельного значения интегралов Френеля.

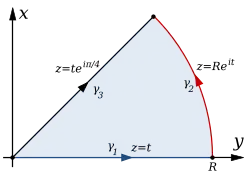
Пределы функций C и S при ${\displaystyle x\rightarrow \infty }$ могут быть найдены с помощью контурного интегрирования. Для этого берётся контурный интеграл функции

${\displaystyle e^{-{\frac {1}{2}}t^{2}}}$

по границе сектора на комплексной плоскости, образованного осью абсцисс, лучом ${\displaystyle y=x}$, ${\displaystyle x\geqslant 0}$ и окружностью радиуса R с центром в начале координат.

При ${\displaystyle R\rightarrow \infty }$ интеграл по дуге стремится к 0, интеграл по вещественной оси стремится к значению интеграла Пуассона

${\displaystyle \int \limits _{0}^{\infty }e^{-{\frac {1}{2}}t^{2}}dt={\sqrt {\frac {\pi }{2}}},}$

и, после некоторых преобразований, интеграл вдоль оставшегося луча может быть выражен через предельное значение интеграла Френеля.

• Дифракция Френеля
• Функция Доусона
• Обобщённые интегралы Френеля

• Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. — New York: Dover, 1972. (См. часть 7)  (англ.)

• Weisstein, Eric W. Fresnel Integrals (англ.) на сайте Wolfram MathWorld.  (англ.)
• Weisstein, Eric W. Cornu Spiral (англ.) на сайте Wolfram MathWorld.  (англ.)
• R. Nave, The Cornu spiral, Hyperphysics (2002) (Использует πt²/2 вместо t².)  (англ.)
• Roller Coaster Loop Shapes (неопр.) (недоступная ссылка). Дата обращения: 13 августа 2008. Архивировано 4 марта 2006 года.  (англ.).