Иллюзия Мюллера-Лайера

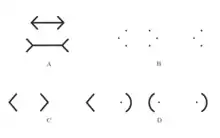
Иллю́зия Мю́ллера-Ла́йера — оптическая иллюзия, возникающая при наблюдении отрезков, обрамлённых стрелками. Иллюзия состоит в том, что отрезок, обрамлённый «остриями», кажется короче отрезка, обрамлённого «хвостовыми» стрелками.

Несмотря на то, что горизонтальные отрезки равной длины, в зависимости от «оперения» их длина представляется разной. Нижняя часть рисунка показывает, что отрезки на самом деле одинаковые.

Иллюзия была впервые описана немецким психиатром Францем Мюллером-Лайером в 1889 году. Несмотря на множество исследований, природа иллюзии не до конца понятна. Наиболее современная трактовка объясняет иллюзию как статистический результат наблюдений внешних изображений — в сценах естественные зрительные элементы, обрамлённые остриями, обычно короче элементов с хвостовым оперением.

Oбъяснения
  • Механизм перспективы — согласно этой трактовке, отрезки воспринимаются как имеющие разную длину, потому что зрительная система интерпретирует расходящиеся линии (например, ближний угол здания) как более удаленные, чем сходящиеся линии (например, дальний угол комнаты). В результате при равных видимых длинах первые кажутся длиннее вторых. Также, если заменить хвостовые оперения на окружности, иллюзия не исчезнет, а перспектива проявится довольно отчетливо.
  • Статистическое объяснение — при наблюдении естественных сцен фигуры, обрамлённые остриями, обычно короче фигур с хвостовым оперением. Зрительная система подстраивается под статистику зрительного окружения и при показе фигур иллюзии Мюллера-Лайера интерпретирует их размеры сообразно накопленной статистике[1].
  • Центроидное объяснение — результаты многочисленных психофизических исследований свидетельствуют о том, что при оценке расстояний между элементами различных изображений зрительная система использует информацию о расстояниях между центрами масс (центроидами) этих изображений взятых целиком[2]. Согласно гипотезе Моргана с соавторами[3], причина этого феномена может быть обусловлена пространственным объединением позиционных сигналов, возникающем вследствие усредняющей суммации паттернов нервного возбуждения, связанных с расположенными по соседству друг с другом элементами изображения. В случае иллюзии Мюллера-Лайера или подобных ей иллюзий протяжённости, зрительная система неспособна определять местоположение ограничительных элементов — терминаторов — стимула (концы базовых линий или вершины крыльев) независимо от соседствующих с ними дистракторов (то есть, самих крыльев или других отвлекающих объектов). В присутствии дистрактора, паттерн вызванного им нейронного возбуждения перекрывается с таковым, вызванным терминатором стимула; тем самым изменяется положение максимума суммарного профиля возбуждения (и, соответственно, смещается его центр масс), что, в итоге, и приводит к искажённому восприятию позиции терминатора, кажущегося смещённым в направлении дистрактора. Эти смещения особенно заметны в динамической фигуре Брентано, предложенной Gianni A. Sarcone[4] (изменения позиций вполне очевидны при фиксации взора на каком-либо из терминаторов), а также в случае вращающихся дистракторов[5]. Общий успех количественного «центроидного» подхода в исследовании геометрических иллюзий, вызванных фигурами, построенными из отрезков линий или отдельных точек[6], подтверждает обоснованность идеи о едином, а именно «центроидном», механизме происхождения широкого круга зрительных искажений восприятия пространственных соотношений.
Классические фигуры Мюллера-Лайера (A) и три модификации (без осевых линий) фигур Брентано, содержащих различные контекстные дистракторы: отдельные точки (B), крылья Мюллера-Лайера (C), дуги окружностей (D)
Фигура Брентано с вращающимися крыльями Мюллера-Лайера; терминаторы стимула (то есть, вершины крыльев) расположены на одной линии на одинаковом расстоянии друг от друга

Зависимость от культурных факторов

Представители разных культур в разной степени подвержены иллюзии Мюллера-Лайера. Так, народы, имеющие меньшее количество прямоугольных предметов (зданий) в зрительном окружении, менее восприимчивы к этой иллюзии[7].

Ссылки
  1. Catherine Q. Howe and Dale Purves. The Müller-Lyer illusion explained by the statistics of image-source relationships. PNAS 102: 1234—1239, 2005.
  2. Whitaker, D., McGraw, P. V., Pacey, I., Barrett, B. T. (1996). Centroid analysis predicts visual localization of first- and second-order stimuli. Vision Research, 36, 2957—2970.
  3. Morgan, M. J., Hole, G. J., & Glennerster, A. (1990). Biases and sensitivities in geometrical illusions. Vision Research, 30, 1793−1810.
  4. Dynamic Müller-Lyer Illusion by Gianni A. Sarcone
  5. Bulatov A., Bertulis A., Mickienė L., Surkys T., Bielevičius A. (2011) Contextual flanks' tilting and magnitude of illusion of extent. Vision Research 51(1), 58−64. https://doi.org/10.1016/j.visres.2010.09.033
  6. Bulatov A., Bulatova N., Surkys T., & Mickienė L . (2015) A quantitative analysis of illusion magnitude changes induced by rotation of contextual distractor. Acta Neurobiologiae Experimentalis, 75, 238−251. http://www.ane.pl/pdf/7520.pdf
  7. Segall MH, Campbell DT, Herkovitz MJ Cultural differences in the perception of geometric illusions. Science. 1963 Feb 22;139:769-71.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.