Изгиб пластин
Изгиб пластин в теории упругости относится к расчёту деформаций в пластинах (в общем случае произвольной толщины, но малым по сравнению с продольными размерами), под действием перпендикулярных к плоскости пластины внешних сил и моментов. Величину отклонения можно определить, решив дифференциальные уравнения соответствующей теории пластин в зависимости от допущений на малость тех или иных параметров. По этим прогибам можно рассчитать напряжения в пластине. При известных напряжениях можно использовать теорию разрушения, чтобы определить, нарушение целостности плиты при данной нагрузке. Деформация пластины является функцией двух координат, поэтому теория пластин формулируется в общем случае в терминах дифференциальных уравнений в двумерном пространстве. Также считается, что пластина изначально (в ненапряжённом состоянии) имеет плоскую форму.
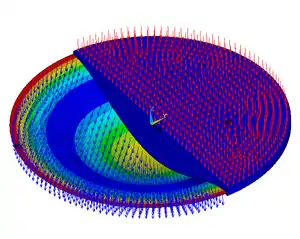
Изгиб пластин в теории Кирхгофа — Лява
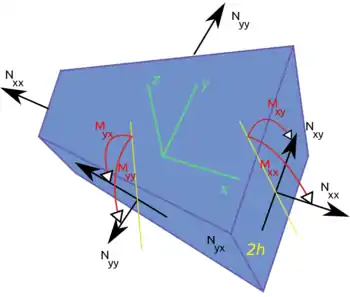
Определения
Для тонкой прямоугольной пластины толщиной , модулем Юнга и коэффициентом Пуассона , можно определить упругие параметры в терминах прогиба пластины .
В декартовой системе координат жёсткость при изгибе определяется
Напряжения
Компоненты изгибных напряжений определяются выражением
Напряжение сдвига задается
Деформации
Изгибающие деформации в теории для малых отклонений определяются
Деформации сдвига в теории для малых отклонений задаются
В теории для больших отклонений пластин рассматривают деформации мембран в виде
Прогибы
Эти прогибы определяются
Вывод
В теории пластин Кирхгофа — Лява система определяющих уравнений состоит из[3]
и
Или в развёрнутой (координатной) форме
и
где приложенная поперечная нагрузка на единицу площади, а толщина плиты равна , напряжения , и
Величина имеет размерность единицы силы на единицу длины. Величина имеет размерность единицы момента на единицу длины.
Для изотропных, однородных пластин с модулем Юнга и коэффициентом Пуассона эти уравнения сводятся к[4]
где прогиб средней поверхности пластины.
Малые прогибы тонких прямоугольных пластин
Малые прогибы тонких прямоугольных пластин описываются уравнением тонкой пластины Жермен — Лагранжа
Это уравнение было впервые выведено Лагранжем в декабре 1811 г. который исправил доклад Софи Жермен.
Большой прогиб тонких прямоугольных пластин
Большой прогиб тонких прямоугольных пластин описывается уравнениями для пластины Феппля — фон Кармана
где функция напряжения.
Круглые пластины Кирхгофа-Лява
Изгиб круглых пластин можно изучить, решив основное уравнение с соответствующими граничными условиями. Эти решения были впервые найдены Пуассоном в 1829 году. Для таких задач удобны цилиндрические координаты. z расстояние точки от средней плоскости пластины.
Основное уравнение в безкоординатной форме имеет вид
В цилиндрических координатах ,
Для симметрично нагруженных круглых пластин, где изгиб зависит от только радиуса получим
Следовательно, основное уравнение приобретёт вид обыкновенного дифференциального уравнения[5]
Если и постоянны, то прямое интегрирование основного уравнения имеет решение
где константы интегрирования. Наклон отклоняющей поверхности равен
Для круглой пластины требование конечности прогиба и крутизны прогиба при подразумевает, что . Однако, не обязательно равняется 0, так как правый предел существует по мере приближения к началу координат .
Закрепленные края
Для круглой пластины (радиуса a) с зажатыми краями и на краю пластины. Подставляя эти граничные условия в общее решение получаем[6]
Смещения пластины в плоскости равны
Плоские деформации в пластине равны
Напряжения в плоскости пластины равны
Для плиты толщиной , жесткость на изгиб и
Результирующие моменты (изгибные моменты) равны
Максимальное радиальное напряжение при и :
где . Изгибающие моменты на границе и в центре пластины равны[7]
Круговая пластина нагруженная силой зависящей от радиуса
Прямоугольные пластины Кирхгофа-Лява
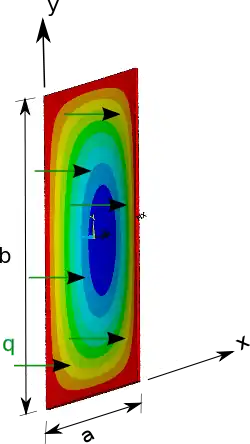
Для прямоугольных пластин Навье в 1820 году ввел простой метод определения смещения и напряжения, когда пластина опирается на края. Идея заключалась в том, чтобы выразить приложенную нагрузку в терминах компонент ряда Фурье, найти решение для синусоидальной нагрузки (одна гармоника Фурье), а затем сложить гармоники Фурье, чтобы получить решение для произвольной нагрузки.
Синусоидальная нагрузка
Предположим, что нагрузка имеет вид[9]
Здесь амплитуда, ширина пластины в направлении и ширина пластины в направлении .
Поскольку пластина просто поддерживается на краях, то смещение на краях пластины равно нулю, и изгибающий момент также равен нулю на границах и , равен нулю на границах и .
При этих граничные условиях и решение уравнения для пластины имеет вид[10]
Где D жесткость на изгиб
Analogous to flexural stiffness EI.[11] Напряжения и деформации в пластине можно рассчитать, если знаем смещение.
При общей нагрузки в виде
где и целые, получим решение[12]
Уравнение для двумерного тригонометрического ряда
Определяем общую нагрузку в виде[12]
где коэффициент Фурье, определяемый формулой[13]
- .
Таким образом, классическое уравнение прямоугольной пластины для малых прогибов принимает следующий вид:
Свободно опёртая пластина с общей нагрузкой
Предполагаем решение вида
Частные дифференциалы этой функции даются выражениями
Подставляя эти выражения в уравнение для пластины, получим
Приравнивая два ряда получим для коэффициентов
или при перестановки получим
Прогиб свободно опертой пластины (на углах) при общей нагрузке задаётся выражением[13]
Свободно опёртая пластина с постоянной нагрузкой
Для равномерно распределенной нагрузки имеем
Таким образом, соответствующий коэффициент Фурье определяется выражением
- .
Вычисляя двойной интеграл, имеем
- ,
или в другом виде кусочно-заданной функции
Прогиб свободно опертой пластины (с условиями на углах) с равномерно распределенной нагрузкой определяется выражением
Изгибающие моменты на единицу длины в пластине определяются выражением
Решение Леви
Другой подход был предложен Леви[14] в 1899 году. В этом случае мы начинаем с предполагаемой формы смещения и пытаемся подогнать параметры так, чтобы выполнялись определяющее уравнение и граничные условия. Цель — найти рашения основного уравнения такие, что они удовлетворяют граничным условиям при и .
Предположим, что[15]
Для пластины, которая свободно опирается краями при и , граничные условия: и . Обратите внимание, что на этих краях нет изменений смещения, что означает и , сводя, таким образом, моментное граничное условие к эквивалентному выражению .
Моменты на краях
Рассмотрим случай чисто моментной нагрузки. В этом случае и функция должна удовлетворять уравнению . в В прямоугольных декартовых координатах основное уравнение выражается как
Подставляем выражение для в основное уравнение что приводит к[16]
или
Это обыкновенное дифференциальное уравнение, имеющее общее решение[17]
где константы, которые можно определить из граничных условий. Следовательно, изгибное решение имеет вид
Выберем систему координат так, чтобы границы пластины находились на краях при и , при . Тогда граничные условия на моменты при
где известные функции. Решение можно найти, используя эти граничные условия. Можно показать, что для симметричного случая, когда
и
получим[18]
где
Аналогично для антисимметричного случая, когда
получим[19]
Используя симметричные и антисимметричные решения, можно составить более общие решения.
Опёртая пластина с равномерно распределенной нагрузкой
Для равномерно распределенной нагрузки
Отклонение опёртой пластины с центром при с равномерно распределенной нагрузкой определяется выражением[20]
Изгибающие моменты на единицу длины в пластине определяются выражениями
Равномерная и симметричная моментная нагрузка
Для частного случая, когда нагрузка симметрична и момент однороден, при ,
Результирующий изгиб равен
где
Изгибающие моменты и поперечные силы, соответствующие смещению находятся по формулам
Напряжения
Изгиб цилиндрической пластины
Цилиндрический изгиб возникает, когда прямоугольная пластина имеющая размеры , где и малую толщину , подвергается равномерной распределенной нагрузке, перпендикулярной плоскости пластины. Такая пластина имеет форму поверхности цилиндра.
С помощью методов Навье и Леви также можно найти решения для свободно опёртых пластин при цилиндрическом изгибе с различным количеством незакреплённых краёв[21].
Изгиб толстых пластин Миндлина
Для толстых пластин необходимо учитывать влияние сдвиговых напряжений по толщине на ориентацию нормали к средней поверхности после деформации. Теория Миндлина предлагает единый подход к нахождению деформации и напряжений в таких пластинах. Решения теории Миндлина можно получить из эквивалентных решений Кирхгофа-Лява с использованием канонических соотношений[22].
Основные уравнения
Канонические уравнения для изотропных толстых пластин можно записать в виде[22]
где приложенная поперечная нагрузка, модуль сдвига, жесткость на изгиб, толщина пластины, , коэффициент поправки сдвигового напряжения, модуль Юнга, коэффициент Пуассона и
Согласно теории Миндлина поперечное смещение средней поверхности пластины, а величины и соответственные повороты нормали к средней поверхности относительно и -осей. Канонические параметры этой теории и . Коэффициент поправки сдвигового напряжения обычно принимают за .
Решения основных уравнений можно найти, если знать соответствующие решения Кирхгофа-Лява с помощью соотношений
где это смещение, предсказанное для пластины Кирхгофа-Лява, бигармоническая функция такая, что , функция, удовлетворяющая уравнению Лапласа, и
Свободно опёртые прямоугольные пластины
Для свободно опертых пластин сумма моментов Маркуса равна нулю
В этом случае функции , , равны нулю, а решение Миндлина связано с соответствующим решением Кирхгофа соотношением
Изгиб консольно-закреплённых пластин Рейсснера-Штейна
Теория Рейсснера-Штейна для консольных пластин[23] приводит к следующим связанным обыкновенным дифференциальным уравнениям для консольной пластины с сосредоточенной нагрузкой на торце в точке .
и граничных условиях в точке
Решение этой системы двух ОДУ дает
где . Изгибные моменты и поперечные силы, соответствующие смещению
Напряжения
Если приложенная нагрузка на краю постоянна, мы восстанавливаем решения для балки при сосредоточенной торцевой нагрузке. Если приложенная нагрузка — линейная функция , то
Ссылки
- Timoshenko et al, 1959, p. 39.
- Timoshenko et al, 1959, p. 82.
- Reddy, J. N., 2007, Theory and analysis of elastic plates and shells, CRC Press, Taylor and Francis.
- Timoshenko, S. and Woinowsky-Krieger, S., (1959), Theory of plates and shells, McGraw-Hill New York.
- Timoshenko et al, 1959, p. 54.
- Timoshenko et al, 1959, p. 55.
- Timoshenko et al, 1959, p. 56.
- Timoshenko et al, 1959, p. 63.
- Timoshenko et al, 1959, p. 105.
- Timoshenko et al, 1959, p. 106.
- Cook, R. D. et al., 2002, Concepts and applications of finite element analysis, John Wiley & Sons
- Timoshenko et al, 1959, p. 108.
- Timoshenko et al, 1959, p. 109.
- Lévy, M., 1899, Comptes rendues, vol. 129, pp. 535—539
- Timoshenko et al, 1959, p. 113.
- Timoshenko et al, 1959, p. 114.
- Timoshenko et al, 1959, p. 180.
- Timoshenko et al, 1959, p. 182.
- Timoshenko et al, 1959, p. 184.
- Timoshenko et al, 1959, p. 116.
- Timoshenko et al, 1959, pp. 180—221.
- Lim, G. T. and Reddy, J. N. О канонических соотношениях для изгиба пластин // International Journal of Solids and Structures. — Т. 40. — С. 3039—3067. — doi:10.1016/S0020-7683(03)00084-2.
- E. Reissner and M. Stein. Torsion and transverse bending of cantilever plates // National Advisory Committee for Aeronautics, Technical Note. — 1951. — Т. 2369. — С. —.
Литература
- S. Timoshenko, S. Woinowsky-Krieger. Теория пластин и оболочек = Theory of plates and shells. — New York: McGraw-Hill, 1959. — 594 с. — ISBN 0-07-085820-9.
.
