Земной прилив

Земной прилив (англ. earth tide ) — колебание тела Земли (смещение уровенной поверхности) под действием приливных сил[1], обусловленных гравитацией Луны и Солнца. Амплитуда смещения около 0,5 метра[1]. Самые значительные периодические составляющие земных приливов — полусуточные, но присутствуют также суточные, полугодовые и двухнедельные колебания.

Сила, вызывающая прилив
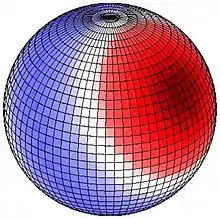
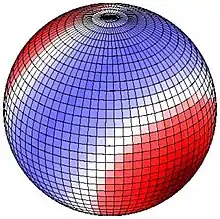
Сила, вызывающая земной прилив: Луна над 30° с. ш.
Сила, вызывающая земной прилив: Луна над 30° ю. ш.

Большая из периодических гравитационных сил исходит от Луны. На рисунках изображена приливная сила, создаваемая Луной, для случая, когда Луна находится точно над над 30° с. ш. (на рисунке справа), или 30° ю. ш. (на рисунке слева. Красным цветом показана сила, направленная вверх (от центра Земли), синим цветом — направленная вниз (к центру Земли). На каждой картинке одна красная область находится под Луной, другая от в противоположной точке. Если, например, Если, например, в данный момент времени Луна находится прямо над 30° с. ш. (правый рисунок), 90° з. д., то центр одной красной области находится на 30° с. ш., 90° з. д. (под Луной), центр второй красной области на 30° ю. ш., 90° в. д. (в противоположной от Луны точке), а синеватой полоса является большим кругом, равноудалённым от этих точек. В результате вращения Земли на 30° широты пик силы возникает один раз в сутки, что дает суточный период колебаний силы. На экваторе же возникновение двух равных пиков (и двух впадин) силы соответствует полусуточному периоду колебаний.

Земной прилив

Земной прилив охватывает все тело Земли, и ему не мешают тонкая кора и массивы суши на поверхности в масштабах, которые делают несущественной жесткость горных пород. Хотя гравитационная сила, вызывающая земные и океанские приливы одинакова, её действие на твёрдую землю и на океанскую воду различна. Океанические приливы являются следствием резонанса одних и тех же движущих сил с периодическими движениями воды в Мировом океане, накопленными за много дней, так что их амплитуда изменяются на коротких расстояниях всего в несколько сотен километров. В то же время периоды собственных колебаний Земли несоразмерны астрономическим временам, поэтому высота земного прилива обусловлена только действующими в данный момента силами.

Компоненты прилива с периодом около двенадцати часов имеют лунную амплитуду (разность высот выпуклости/впадины земной поверхности), которая чуть более чем в два раза превышает высоту солнечных амплитуд, как показано в таблице ниже. Полусуточный прилив (один максимум каждые 12 или около того часов) преимущественно лунный и вызывает секторальные деформации. Суточный прилив лунно-солнечный и вызывает тессеральные деформации[2].

Приливные составляющие

Основные составляющие прилива. Амплитуды могут отличаться от перечисленных в пределах нескольких процентов[3][4]

Полусуточный

Приливная составляющая Период Вертикальная амплитуда (мм) Горизонтальная амплитуда (мм)
М 2 12,421 ч 384,83 53,84
S 2 (солнечная полусуточная) 12.000 ч 179,05 25.05
N 2 12,658 ч 73,69 10.31
К 2 11,967 ч 48,72 6,82

Дневной

Приливная составляющая Период Вертикальная амплитуда (мм) Горизонтальная амплитуда (мм)
К 1 23,934 ч 191,78 32.01
О 1 25,819 ч 158,11 22.05
Р 1 24,066 ч 70,88 10.36
ф 1 23,804 ч 3,44 0,43
ψ 1 23,869 ч 2,72 0,21
S 1 (солнечно-суточный) 24.000 ч 1,65 0,25

Долгосрочный

Приливная составляющая Период Вертикальная амплитуда (мм) Горизонтальная амплитуда (мм)
М ф 13 661 дней 40,36 5,59
М м (лунный месяц) 27 555 дней 21.33 2,96
S sa (солнечное полугодие) 0,50000 лет 18,79 2,60
Лунный узел 18 613 лет 16,92 2,34
S a (солнечный годовой) 1.0000 лет 2,97 0,41

Следствия земных приливов

Вы­со­ко­точ­ные дан­ные о зем­ных при­ли­вах бы­ли по­лу­че­ны с по­мо­щью крио­ген­ных гравиметров, а так­же ра­дио­ин­тер­фе­ро­мет­ров со сверх­длин­ной ба­зой[1]. Вулканологи используют регулярные, предсказуемые движения земных приливов для калибровки и тестирования чувствительных инструментов мониторинга деформации вулканов. Приливы также могут вызывать вулканические явления[5].

Амплитуду земных приливов важно учитывать в глобальной системе позиционирования, и в измерениях спутниковой лазерной локации. Земные приливы также необходимо учитывать в случае некоторых экспериментов по физике элементарных частиц, например, в ЦЕРН[6] или Национальной ускорительной лаборатории SLAC очень большие ускорители частиц были спроектированы с учетом земных приливов для правильной работы[7].

Приливы в планетах и лунах, а также у двойных звезд и двойных астероидов играют ключевую роль в их динамике планетарных. Например, из-за приливного колебания Луна попадает в спин-орбитальный резонанс 1:1, в силу чего она всегда повёрнута к Земле одной стороной. Из-за прилива так же и Меркурий находится в ловушке спин-орбитального резонанса 3:2 с Солнцем[8]. По той же причине считается, что многие экзопланеты захвачены в более высоких спин-орбитальные резонансы со своими родительскими звездами[9].

Литература

Примечания
  1. Молоденский С. М. Приливы и отливы, 2015.
  2. Мельхиор П. Земные приливы, 1968.
  3. John Wahr, "Earth Tides", Global Earth Physics, A Handbook of Physical Constants, AGU Reference Shelf, 1, pp. 40–46, 1995.
  4. Michael R. House, "Orbital forcing timescales: an introduction", Geological Society, London, Special Publications; 1995; v. 85; p. 1-18. http://sp.lyellcollection.org/cgi/content/abstract/85/1/1
  5. Sottili G., Martino S., Palladino D.M., Paciello A., Bozzano F. (2007), Effects of tidal stresses on volcanic activity at Mount Etna, Italy, Geophys. Res. Lett., 34, L01311, doi:10.1029/2006GL028190, 2007.
  6. Мельхиор П. Земные приливы, 1968, с. 315-317.
  7. Accelerator on the move, but scientists compensate for tidal effects, Stanford online
  8. Noyelles, B. (2014). “Spin-orbit evolution of Mercury revisited”. Icarus. 241: 26—44. arXiv:1307.0136. Bibcode:2014Icar..241...26N. DOI:10.1016/j.icarus.2014.05.045.
  9. Makarov, V. V. (2012). “Dynamical Evolution and Spin–Orbit Resonances of Potentially Habitable Exoplanets: The Case of GJ 581d”. The Astrophysical Journal. 761 (2): 83. arXiv:1208.0814. Bibcode:2012ApJ...761...83M. DOI:10.1088/0004-637X/761/2/83. 83.

 

См. также
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.