Закон Гесса

Закон Гесса — основной закон термохимии, который формулируется следующим образом:

Тепловой эффект химической реакции, проводимой в изобарно-изотермических или изохорно-изотермических условиях, зависит только от вида и состояния исходных веществ и продуктов реакции и не зависит от пути её протекания.

Иными словами, количество теплоты, выделяющееся или поглощающееся при каком-либо процессе (при p,T = const или V,T = const), всегда одно и то же, независимо от того, протекает ли данное химическое превращение в одну или в несколько стадий (при условии, что температура, давление и агрегатные состояния веществ одинаковы). Например, окисление глюкозы в организме осуществляется по очень сложному многостадийному механизму, однако суммарный тепловой эффект всех стадий данного процесса равен теплоте сгорания глюкозы. Иными словами, закон Гесса есть утверждение о том, что тепловой эффект реакции (Q_p = ΔH_p,T или Q_V=ΔU_V,T) является функцией состояния. Тепловой эффект реакции (который определён только для изобарно-изотермического или для изохорно-изотермического процессов) нельзя путать с теплотой (Q), выделяемой или поглощаемой в ходе процесса или реакции. В общем случае теплота не является функцией состояния и не описывается законом Гесса.

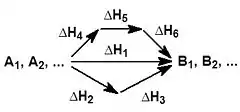
На рисунке приведено схематическое изображение некоторого обобщенного химического процесса превращения исходных веществ А₁, А₂… в продукты реакции В₁, В₂…, который может быть осуществлен различными путями в одну, две или три стадии, каждая из которых сопровождается тепловым эффектом ΔH_i. Согласно закону Гесса, тепловые эффекты всех этих реакций связаны следующим соотношением:

\Delta H_{1}=\Delta H_{2}+\Delta H_{3}=\Delta H_{4}+\Delta H_{5}+\Delta H_{6}.

Закон открыт русским химиком Г. И. Гессом в 1841 году; он является частным случаем первого начала термодинамики применительно к химическим реакциям. Практическое значение закона Гесса состоит в том, что он позволяет рассчитывать тепловые эффекты самых разнообразных химических процессов; для этого обычно используют ряд следствий из него.

Следствия из закона Гесса

Тепловой эффект прямой реакции равен по величине и противоположен по знаку тепловому эффекту обратной реакции (закон Лавуазье — Лапласа).

Тепловой эффект химической реакции равен разности сумм теплот образования (ΔH_f) продуктов реакции и исходных веществ, умноженных на стехиометрические коэффициенты (ν):

\Delta H^{o}=\sum {(\nu }_{i}\Delta H_{f,i}^{o})_{products}-\sum {(\nu }_{i}\Delta H_{f,i}^{o})_{reactants}.

Тепловой эффект химической реакции равен разности сумм теплот сгорания (ΔH_c) исходных веществ и продуктов реакции, умноженных на стехиометрические коэффициенты (ν):

\Delta H^{o}=\sum {(\nu }_{i}\Delta H_{c,i}^{o})_{reactants}-\sum {(\nu }_{i}\Delta H_{c,i}^{o})_{products}.

Таким образом, пользуясь табличными значениями теплот образования или сгорания веществ, можно рассчитать теплоту реакции, не прибегая к эксперименту. Табличные величины теплот образования и сгорания веществ обычно относятся к т. н. стандартным условиям. Для расчёта теплоты процесса, протекающего при иных условиях, необходимо использовать и другие законы термохимии, например, закон Кирхгофа, описывающий зависимость теплового эффекта реакции от температуры

Если начальное и конечное состояния химической реакции (реакций) совпадают, то их тепловой эффект равен нулю.

Примеры применения

Пример 1.

Вопрос:

Найти энергию кристаллической решётки хлорида калия.

Дано:

ΔH_{f, 298}(KCl) = -435,56 kJ/mol
ΔH_{298 атомизации}(K (s)) = 128,74 kJ/mol
ΔH_{298 ионизации}(K (g)) = 418 kJ/mol
ΔH_{298 диссоциации}(Cl₂ (g)) = 238,26 kJ/mol

Сродство хлора к электрону = -363,66 kJ/mol

По определению, каждая из указанных величин - точно так же, как изменения энтальпий реакций образования веществ (которые кратко на химическом профессиональном жаргоне называют "энтальпии веществ" или "энтальпии образования веществ") и точно так же, как изменения энтальпий реакций сгорания веществ (на профессиональном жаргоне "энтальпии сгорания") - точно так же и эти тепловые эффекты характеризуют каждый определённую реакцию. Для начала, выписываем эти реакции, закреплённые за названиями тепловых эффектов (для удобства реакции ниже будут пронумерованы):

ΔH_{f, 298}(KCl) характеризует реакцию (№1) образования KCl из простых веществ, устойчивых при данных p, T:

K (s) + 0,5Cl₂ (g) → KCl (s)

ΔH_{298 атомизации}(K (s)) характеризует реакцию (№2):

K (s) → K (g)

ΔH_{298 ионизации}(K (g)) характеризует реакцию (№3):

K (g) → K⁺ + e^–(g)

ΔH_{298 диссоциации}(Cl₂ (g)) характеризует реакцию (№4):

Cl₂ (g) → 2Cl (g)

Сродство хлора к электрону характеризует реакцию (№5):

Cl (g) + e^–(g) → Cl^–(g)

Задача заключается в том, чтобы из этих уравнений реакций сложить заданное уравнение реакции - энергия кристаллической решётки KCl характеризует реакцию (№6):

K⁺ + Cl^–(g) → KCl (s)

Для этого возьмём реакции в такой комбинации: №6 = №1 + (–0,5)№4 + (–1)№5 + (–1)№2 + (–1)№3 = №1 – 0,5№4 – №5 – №2 – №3. При сложении уравнений реакций тепловые эффекты складываются (с теми же коэффициентами, на которые умножали реакции). То есть ΔH₆ = ΔH₁ – 0,5ΔH₄ – ΔH₅ – ΔH₂ – ΔH₃

K (s) + 0,5Cl₂ (g) → KCl (s)
(K (s) → K (g))⋅(–1) = (K (g) → K (s))
K⁺ + e^–(g) →K (g)
Cl^–(g) → Cl (g) + e^–(g)
Cl (g) → 0,5Cl₂ (g)

Сумма этих реакций:

K (s) + Cl₂ (g) + K (g) + K⁺ + e^–(g) + Cl^–(g) + Cl (g) → 0,5Cl₂ (g) + Cl (g) + e^–(g) + K (g) + K (s) + KCl (s)

После сокращения получаем:

K⁺ + Cl^–(g) → KCl (s)

Что и требовалось - значит, суммирование реакций произведено верно и полученный суммарный тепловой эффект характеризует именно искомую реакцию.

Пример 2.

Дано:

B₂O₃ (s) + 3H₂O (g) → 3O₂ (g) + B₂H₆ (g) (ΔH = 2035 kJ/mol)
H₂O (l) → H₂O (g) (ΔH = 44 kJ/mol)
H₂ (g) + (1/2)O₂ (g) → H₂O (l) (ΔH = -286 kJ/mol)
2B (s) + 3H₂ (g) → B₂H₆ (g) (ΔH = 36 kJ/mol)

Найти ΔH_f реакции:

2B (s) + (3/2) O₂ (g) → B₂O₃ (s)

После умножения реакций на числа (в том числе на -1, то есть обращения реакций), а соответственно – и умножения на те же числа изменений энтальпии этих реакций, получаем:

B₂H₆ (g) + 3O₂ (g) → B₂O₃ (s) + 3H₂O (g) (ΔH = -2035 kJ/mol)
3H₂O (g) → 3H₂O (l) (ΔH = -132 kJ/mol)
3H₂O (l) → 3H₂ (g) + (3/2) O₂ (g) (ΔH = 858 kJ/mol)
2B (s) + 3H₂ (g) → B₂H₆ (g) (ΔH = 36 kJ/mol)

После сложения этих уравнений реакций и приведения подобных членов получившегося уравнения, получаем:

2B (s) + (3/2) O₂ (g) → B₂O₃ (s) (ΔH = -1273 kJ/mol)

Литература

Карапетьянц М. Х. Введение в теорию химических процессов. — М.: Высшая школа, 1981. 304 с.
Стромберг А. Г., Семченко Д. П. Физическая химия — М.: Высшая школа, 1999. 527 с.
Даниэльс Ф., Олберти Р. Физическая химия — М.: Мир, 1978. 645 с.
Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур. — М.: Мир, 2002. 461 с.
Борисов И. М. Основы электрохимии: учеб. пособие. -Уфа: Изд-во БГПУ, 2009.- 115 с.

Ссылки

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.