Задача о стопке кирпичей
Задача о стопке кирпичей, также известна как проблема укладки блоков (англ. Block-stacking problem), наклонная башня лир (англ. The Leaning Tower of Lire), задача о складывании книг и т. д. — задача статики, заключающаяся в укладке прямоугольных блоков в башню, как можно дальше выдающуюся в сторону.
Формулировка
Проблема формулируется так:
Поставить друг на друга одинаковых твёрдых прямоугольных параллелепипедов, собрав устойчивую башню на краю стола таким образом, чтобы выступ за край был максимален.
История

Задача о стопке кирпичей имеет долгую историю как в механике, так и в математике. В своих статьях Майк Патерсон (англ. Mike Paterson) и его соавторы приводят[1] длинный список ссылок на эту проблему, о которой говорится в работах по механике, относящихся к середине девятнадцатого века.
Решения
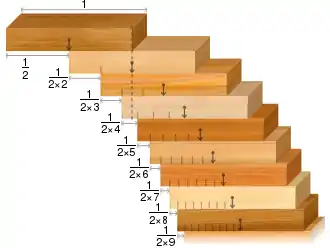
С только одним блоком на каждом уровне
В идеальном случае с только одним идеально прямоугольным блоком на каждом уровне свес равен ширины блока[2]. Эта сумма составляет половину частичной суммы гармонического ряда. Поскольку гармонический ряд расходится, максимальный свес стремится к бесконечности с ростом , т.е. можно достичь любого сколь угодно большого свеса при достаточном количестве блоков. В каждом конкретном случае максимальный свес приблизительно равен , т.е. пропорционален натуральному логарифму числа блоков.
| N | Максимальный свес | |||
|---|---|---|---|---|
| дробь | десятичная запись | относительный размер | ||
| 1 | 1 | /2 | 0,5 | |
| 2 | 3 | /4 | 0,75 | |
| 3 | 11 | /12 | ~0,91667 | |
| 4 | 25 | /24 | ~1,04167 | |
| 5 | 137 | /120 | ~1,14167 | |
| 6 | 49 | /40 | 1,225 | |
| 7 | 363 | /280 | ~1,29643 | |
| 8 | 761 | /560 | ~1,35893 | |
| 9 | 7 129 | /5 040 | ~1,41448 | |
| 10 | 7 381 | /5 040 | ~1,46448 | |
| N | Максимальный свес | |||
|---|---|---|---|---|
| дробь | десятичная запись | относительный размер | ||
| 11 | 83 711 | /55 440 | ~1,50994 | |
| 12 | 86 021 | /55 440 | ~1,55161 | |
| 13 | 1 145 993 | /720 720 | ~1,59007 | |
| 14 | 1 171 733 | /720 720 | ~1,62578 | |
| 15 | 1 195 757 | /720 720 | ~1,65911 | |
| 16 | 2 436 559 | /1 441 440 | ~1,69036 | |
| 17 | 42 142 223 | /24 504 480 | ~1,71978 | |
| 18 | 14 274 301 | /8 168 160 | ~1,74755 | |
| 19 | 275 295 799 | /155 195 040 | ~1,77387 | |
| 20 | 55 835 135 | /31 039 008 | ~1,79887 | |
| N | Максимальный свес | |||
|---|---|---|---|---|
| дробь | десятичная запись | относительный размер | ||
| 21 | 18 858 053 | /10 346 336 | ~1,82268 | |
| 22 | 19 093 197 | /10 346 336 | ~1,84541 | |
| 23 | 444 316 699 | /237 965 728 | ~1,86715 | |
| 24 | 1 347 822 955 | /713 897 184 | ~1,88798 | |
| 25 | 34 052 522 467 | /17 847 429 600 | ~1,90798 | |
| 26 | 34 395 742 267 | /17 847 429 600 | ~1,92721 | |
| 27 | 312 536 252 003 | /160 626 866 400 | ~1,94573 | |
| 28 | 315 404 588 903 | /160 626 866 400 | ~1,96359 | |
| 29 | 9 227 046 511 387 | /4 658 179 125 600 | ~1,98083 | |
| 30 | 9 304 682 830 147 | /4 658 179 125 600 | ~1,99749 | |
С несколькими блоками на любом из уровней

Дополнительные блоки на уровне могут использоваться как противовес и давать бо́льшие свесы, чем вариант с одним блоком на уровне. Даже для трех блоков укладка двух уравновешенных блоков поверх другого блока может дать свес в один блок, в то время как в простом идеальном случае — не более . В 2007 году Майк Патерсон с соавторами показали[1], что максимальный свес, который может быть достигнут с помощью нескольких блоков на уровне, асимптотически равен , то есть пропорционален кубическому корню из числа блоков, в отличие от простого случая, когда свес пропорционален логарифму количества блоков.
См. также
Примечания
- Paterson et al, 2009.
- Здесь — номер блока; нумерация ведётся, начиная с верхнего.
Ссылки
- Weisstein, Eric W. Book Stacking Problem (англ.) на сайте Wolfram MathWorld.
- Building an Infinite Bridge. PBS Infinite Series (4 мая 2017). Дата обращения: 3 сентября 2018.
- Mike Paterson, Yuval Peres, Mikkel Thorup, Peter Winkler, and Uri Zwick. Maximum Overhang // American Mathematical Monthly. — 2009. — Vol. 116. — P. 763–787.