Дифференциальный бином
В математическом анализе дифференциальным биномом или биномиальным дифференциалом называется дифференциал вида
где a, b — действительные числа, a m, n, p — рациональные числа. Представляет интерес интеграл от дифференциального бинома:
Свойства
Выразимость интеграла в элементарных функциях
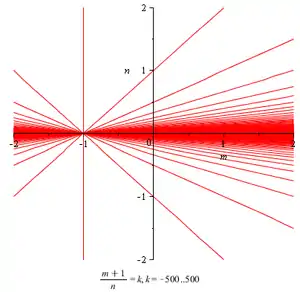
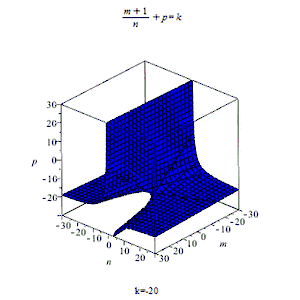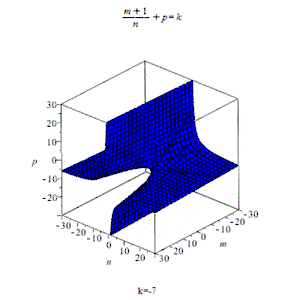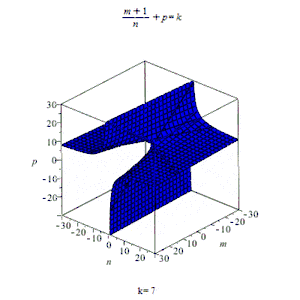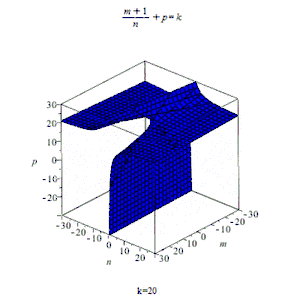
Интеграл от дифференциального бинома выражается в элементарных функциях только в трёх случаях:
- — целое число. Используется подстановка , — общий знаменатель дробей и ;
- — целое число. Используется подстановка , — знаменатель дроби .
- — целое число. Используется подстановка , — знаменатель дроби .
Связь с бета-функцией и гипергеометрической функцией
Интеграл от дифференциального бинома выражается через неполную бета-функцию:
где , а также через гипергеометрическую функцию:
Примеры
Интеграл
не выражается в элементарных функциях, здесь , и ни одно из трёх условий для m, n и p не выполнено.
В то же время интеграл
- ,
как видим, выражается в элементарных функциях, поскольку здесь , и , то есть является целым числом.
История

Случаи выразимости дифференциального бинома в элементарных функциях были известны ещё Л. Эйлеру. Однако, невыразимость дифференциального бинома в элементарных функциях во всех остальных случаях была доказана П. Л. Чебышёвым в 1853 году[1].
См. также
Примечания
- P. Tchebichef. Sur l'intégration des différentielles irrationnelles (фр.) // Journal de mathématiques pures et appliquées : magazine. — 1853. — Vol. XVIII. — P. 87—111.
Ссылки
- Дифференциальный бином — статья из Большой советской энциклопедии.
- Integration Of Differential Binomial (англ.) на сайте PlanetMath.
- Tables of indefinite integrals.