Двугранный угол
Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями[1].


Определения и свойства
Полуплоскости называются гранями двугранного угла, а их общая прямая — ребром.
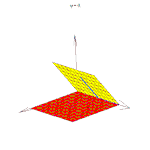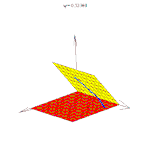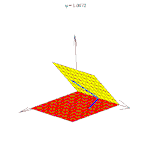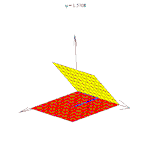
Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. Таким образом, чтобы измерить двугранный угол, можно взять любую точку на его ребре и перпендикулярно ребру провести из неё лучи в каждую из граней. Линейный угол между этими двумя лучами и будет равен по величине двугранному углу. Если один из лучей не перпендикулярен ребру, то величина линейного угла между лучами в общем случае будет отлична от величины двугранного угла. Например, в любой двугранный угол (в том числе больший 90 градусов) можно поместить прямой угол так, чтобы его вершина лежала на ребре двугранного угла, а стороны принадлежали его граням. В этом легко убедиться, размещая угольник в приоткрытой книге.
У всякого многогранника, правильного или неправильного, выпуклого или вогнутого, есть двугранный угол на каждом ребре.
Величины двугранных углов правильных многогранников:
| Название | точный двугранный угол в радианах | приближённое значение в градусах |
|---|---|---|
| Тетраэдр | arccos(1/3) | 70.53° |
| Гексаэдр или куб | π/2 | 90°(точн.) |
| Октаэдр | π − arccos(1/3) | 109.47° |
| Додекаэдр | 2·arctg(φ) | 116.56° |
| Икосаэдр | 2·arctg(φ + 1) | 138.19° |
где φ = (1 + √5)/2 — золотое сечение.
Вариации и обобщения
- Двугранным углом также называется пересечение двух полупространств в -мерном Евклидовом пространстве.
Примечания
- Д’Аламбера оператор — Кооперативная игра // «Математическая энциклопедия» / Главный редактор И. М. Виноградов. — М.: «Советская энциклопедия», 1979. — Т. 2. — С. 50. — 1104 с. — (51[03] М34). — 148 800 экз.