Граф Фрухта
Граф Фрухта — один из двух минимальных кубических графов, не имеющих нетривиальных автоморфизмов. Описан Робертом Фрухтом в 1939.[1]
| Граф Фрухта | |
|---|---|
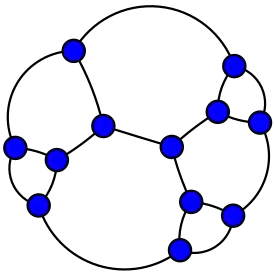 | |
| Назван в честь | Роберта Фрухта |
| Вершин | 12 |
| Рёбер | 18 |
| Радиус | 3 |
| Диаметр | 4 |
| Обхват | 3 |
| Автоморфизмы | 1 (тождественный) |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Свойства |
кубический планарный гамильтонов |
Свойства
Граф Фрухта:
- Имеет 12 вершин и 18 рёбер;
- Является кубическим графом;
- Является рёберно k-связным графом;
- Имеет радиус 3, диаметр 4, обхват 3, хроматическое число 3, хроматический индекс 3, число независимости равно 5;
- Граф Фрухта является гамильтоновым и задётся LCF-кодом
 Раскраска в три цвета.
Раскраска в три цвета.
- Граф Фрухта — это граф Халина.
- Как и все графы Халина, граф Фрухта является планарным, 3-вершинно-связным и графом многогранника.
- Граф Фрухта — один из двух минимальных кубических графов, имеющих единственный автоморфизм — тождественность[3] (таким образом, любая вершина может быть топологически отличима от остальных). Такие графы называются асимметричными графами.
- Теорема Фрухта утверждает, что любую группу можно представить как группу симметрий графа,[1] а усиление этой теоремы, тоже Фрухта, утверждает, что любая группа может быть представлена как группа симметрий 3-регулярного графа[4] Граф Фрухта даёт пример такой реализации для тривиальной группы.
- Характеристический многочлен графа Фрухта равен .
Ссылки
- R. Frucht. Herstellung von Graphen mit vorgegebener abstrakter Gruppe. // Compositio Mathematica. — 1939. — Т. 6. — С. 239–250. — ISSN 0010-437X..
- Weisstein, Eric W. Frucht Graph (англ.) на сайте Wolfram MathWorld.
- Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, 1990
- R. Frucht. Graphs of degree three with a given abstract group // Canadian Journal of Mathematics. — 1949. — Т. 1. — С. 365–378. — ISSN 0008-414X. — doi:10.4153/CJM-1949-033-6..
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.