Гипотеза Эрдёша — Фабера — Ловаса
Гипотеза Эрдёша — Фабера — Ловаса — это проблема о раскраске графов, названная именами Пала Эрдёша, Ванса Фабера и Ласло Ловаса, которые сформулировали её в 1972 году[1]. Гипотеза гласит:
- Если k полных графов, каждый из которых имеет в точности k вершин, обладают свойством, что любая пара полных графов имеет не более одной общей вершины, то объединение графов может раскрашено в k цветов.
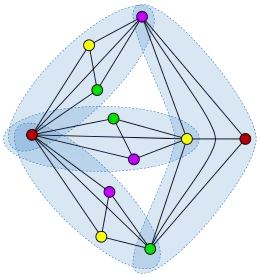
В 2021 году был опубликован препринт с доказательством гипотезы для больших k[2].
Эквивалентные формулировки
Аддад и Тардиф[3] представили задачу с историей о создании комитета — представим, что в университетском факультете имеется k комитетов, каждый состоящий из k членов, и все комитеты используют ту же комнату, имеющую k кресел. Предположим, что имеется не более одного человека, входящего в любые два комитета. Можно ли назначить каждому члену комитета кресло таким образом, что каждый член сидит на одном и том же кресле во всех комитетах? В этой модели задачи члены комитетов соответствуют вершинам графа, комитеты соответствуют полным графам, а кресла соответствуют цветам.
Линейный гиперграф (известный также как частично линейное пространство), это гиперграф, имеющей свойство, что любые два гиперребра имеют не более одной вершины. Говорят, что гиперграф является однородным, если все его гиперрёбра имеют одинаковое число составляющих вершин. В гипотезе Эрдёша — Фабера — Ловаса n клик размера n можно интерпретировать как гиперребра n-однородного линейного гиперграфа, который имеет те же вершины, что и лежащий в основе граф. На этом языке гипотеза Эрдёша — Фабера — Ловаса утверждает, что если любой n-однородный линейный гиперграф с n гиперрёбрами, можно раскрасить в n цветов вершины таким образом, что каждое гиперребро имеет одну вершину каждого цвета[4].
Простой гиперграф — это гиперграф, в котором не более одного ребра соединяет любую пару вершин и нет гиперрёбер размера единица. В формулировке гипотезы Эрдёша — Фабера — Ловаса на языке раскраски графов можно без проблем удалить вершины, принадлежащие лишь одной клике, поскольку их раскраска трудностей не вызывает. После того как это сделано, гиперграф, который имеет в качестве вершин клики, а в качестве гиперрёбер вершины графа, является простым гиперграфом. Гиперграф, двойственный раскраске вершин, это рёберная раскраска. Таким образом, гипотеза Эрдёша — Фабера — Ловаса эквивалентна утверждению, что любой простой гиперграф с n вершинами имеет хроматический индекс (число цветов рёберной раскраски), не превосходящий n[5].
Граф в гипотезе Эрдёша — Фабера — Ловаса можно представить как граф пересечений множеств — каждой вершине графа соответствует множество клик, содержащих вершину, и любые две вершины соединены ребром, если их соответствующие множества имеют непустое пересечение. Используя это описание графа, гипотезу можно поставить следующим образом: если некоторое семейство имеет в общей сложности n элементов и любые два множества в пересечении имеют не более одного элемента, граф пересечений этих множеств можно раскрасить в n цветов[6].
Число пересечений графа G равно минимальному числу элементов в семействе множеств, граф пересечений которых совпадает с G, или, эквивалентно, минимальному числу вершин гиперграфа, рёберный граф которого совпадает с G. Кляйн и Марграф[7] определяют аналогично линейное число пересечений графа как минимальное число вершин в линейном гиперграфе, рёберный граф которого совпадает с G. Как они замечают, гипотеза Эродёша — Фабера Ловаса эквивалентна утверждению, что хроматическое число любого графа не превосходит его линейного числа пересечений.
Хаддад и Тардиф[3] дают другую, но всё же эквивалентную, формулировку в терминах теории клонов.
История и частичные результаты
Пал Эрдёш, Ванс Фабер и Ласло Ловас сформулировали гипотезу в 1972[1]. Пал Эрдёш первоначально предложил $50 за доказательство верности гипотезы, а позднее увеличил вознаграждение до $500[1][8].
Чианг и Лоулер[9] доказали, что хроматическое число графа в гипотезе не превосходит 3k/2 − 2, а Кан[10] улучшил эту величину до k + o(k).
Связанные задачи
Интересно также рассмотреть хроматическое число графов, образованных объединением k клик с k вершинами в каждой без ограничения размера пересечения пар клик. В этом случае хроматическое число их объединения не превосходит и некоторые графы, образованные таким образом, требуют именно такого количества цветов[11][12].
Известно, что версия гипотезы, использующая дробное хроматическое число вместо хроматического числа, верна. То есть, если граф G образован объединением k k-клик, которые попарно пересекаются не более чем в двух вершинах, граф G может быть раскрашен в k-цветов[13].
В случае рёберной раскраски простых гиперграфов Хиндман[6] определяет число L для простого гиперграфа как число вершин гиперграфа, принадлежащих гиперребру с тремя и более вершинами. Он показал, что для любого фиксированного значения L проверка, что гипотеза верна для всех простых графов с , требует конечного количества вычислений. Основываясь на этой идее, он показал, что гипотеза верна для всех простых гиперграфов с . В формулировке раскраски графов, образованных объединением клик, результат Хиндмана показывает, что гипотеза верна, если не более десяти клик содержат вершины, принадлежащие трём или более кликам. В частности, это верно для .
Примечания
- Erdős, 1981.
- Kelsey Houston-Edwards. Mathematicians Settle Erdős Coloring Conjecture (англ.). Quanta (5 апреля 2021). Дата обращения: 5 апреля 2021.
- Haddad, Tardif, 2004.
- Romero, Sánchez Arroyo, 2007.
- Chiang, Lawler, 1988. Хиндман ((Hindman 1981)) описывает эквивалентную задачу на языке системы множеств вместо гиперграфов.
- Hindman, 1981.
- Klein, Margraf, 2003.
- Chung, Graham, 1998.
- Chiang, Lawler, 1988.
- Kahn, 1992.
- Erdős, 1991.
- Horák, Tuza, 1990.
- Kahn, Seymour, 1992.
Литература
- Chiang W. I., Lawler E. L. Edge coloring of hypergraphs and a conjecture of Erdős, Faber, Lovász // Combinatorica. — 1988. — Т. 8, вып. 3. — С. 293–295. — doi:10.1007/BF02126801.
- Fan Chung, Ronald Graham. Erdős on Graphs: His Legacy of Unsolved Problems. — A K Peters, 1998. — С. 97–99.
- Paul Erdős. On the combinatorial problems which I would most like to see solved // Combinatorica. — 1981. — Т. 1. — С. 25–42. — doi:10.1007/BF02579174.
- Paul Erdős. Advanced problem 6664 // American Mathematical Monthly. — Mathematical Association of America, 1991. — Т. 98, вып. 7. — С. 655. — doi:10.2307/2324942. — . Solutions by Ilias Kastanas, Charles Vanden Eynden, and Richard Holzsager, American Mathematical Monthly 100 (7): 692–693, 1992.
- Haddad L., Tardif C. A clone-theoretic formulation of the Erdős-Faber-Lovasz conjecture // Discussiones Mathematicae Graph Theory. — 2004. — Т. 24. — С. 545–549. Архивировано 6 июля 2011 года.
- Neil Hindman. On a conjecture of Erdős, Faber, and Lovász about n-colorings // Can. J. Math.. — 1981. — Т. 33, вып. 3. — С. 563–570. — doi:10.4153/CJM-1981-046-9.
- Horák P., Tuza Z. A coloring problem related to the Erdős–Faber–Lovász conjecture // Journal of Combinatorial Theory, Series B. — 1990. — Т. 50, вып. 2. — С. 321–322. — doi:10.1016/0095-8956(90)90087-G.. Исправленная версия JCTB 51 (2): 329, 1991 с добавлением Туза в качестве соавтора
- Jeff Kahn. Coloring nearly-disjoint hypergraphs with n + o(n) colors // Journal of Combinatorial Theory, Series A. — 1992. — Т. 59. — С. 31–39. — doi:10.1016/0097-3165(92)90096-D.
- Jeff Kahn, Paul Seymour. A fractional version of the Erdős-Faber-Lovász conjecture // Combinatorica. — 1992. — Т. 12, вып. 2. — С. 155–160. — doi:10.1007/BF01204719.
- Hauke Klein, Marian Margraf. On the linear intersection number of graphs. — 2003.
- David Romero, Abdón Sánchez Arroyo. Combinatorics, Complexity, and Chance : A Tribute to Dominic Welsh / Geoffrey Grimmet, Colin McDiarmid. — Oxford University Press, 2007. — С. 285–298. — doi:10.1093/acprof:oso/9780198571278.003.0017.