Волны Рэлея
Во́лны Рэле́я — поверхностные акустические волны. Названы в честь Рэлея, теоретически предсказавшего их в 1885 году[1].
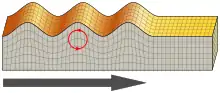
Описание
Волны Рэлея распространяются вблизи поверхности твердого тела. Фазовая скорость таких волн направлена параллельно поверхности. Частицы среды в такой волне совершают эллиптическое движение в сагиттальной плоскости (в которой лежат вектор скорости и нормали к поверхности). Амплитуды колебаний затухают при удалении от поверхности по экспоненциальным законам и энергия волны сосредоточена в области на расстоянии порядка длины волны от поверхности[2].
Волна Рэлея в изотропном теле
Уравнение движения бесконечно малого объёма однородной, изотропной и идеально упругой среды с плотностью ρ можно записать в виде:
| (1) |
где U — смещение бесконечного малого объёма относительно равновесного положения, λ и μ — упругие постоянные, Δ — оператор Лапласа. Для данного волнового уравнения решения ищутся в виде суперпозиции поперечных и продольных смещений U=Ut+Ul, где Ul=grad φ и Ut=rot ψ. φ и ψ — скалярный и векторный потенциалы. Уравнение (1) для новых неизвестных представляет собой волновые уравнения для независимых компонент смещений[3]:
| (2.1) |
| (2.2) |
Если волна распространяется по оси x, то можно рассмотреть для изотропного случая только колебания в плоскости (x, z). Принимая во внимание независимость компонент от y для плоской гармонической волны, волновые уравнения для потенциалов примут вид:
| (3.1) |
| (3.2) |
где — волновые числа для продольных и поперечных волн. Решения этих уравнений, если взять только затухающие решения представляются в виде плоских волн[4]:
| (4.1) |
| (4.2) |
где ; ; ; A и B — произвольные постоянные. Эти решения представляют собой общее решение волнового уравнения для затухающей волны, а для нахождения частного решения нужно задать граничные условия на поверхности среды.
Компоненты смещения представляются в виде:
| (5.1) |
| (5.1) |
В случае свободной границы значение компонентов тензора напряжений принимают нулевые значение:
| (6.1) |
| (6.2) |
После подставления решений (4) получится однородная система линейных уравнений относительно амплитуд A и B, которая имеет нетривиальное решение только если детерминант системы равен нулю (уравнение Рэлея), а именно[5]:
| (6) |
где , . Это уравнение имеет единственный корень, относящийся к рэлеевской волне, который зависит только от коэффициента Пуассона ν:
| (7) |
Отсюда находятся компоненты смещений для рэлеевской волны[6]:
| (8.1) |
| (8.2) |
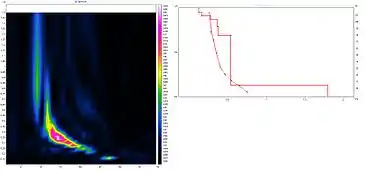
Практическое применение волн рэлеевского типа
Волны рэлеевского типа (псевдорэлеевские волны) успешно применяются в инженерной сейсморазведке для изучения упругих параметров пород и грунтов находящихся за обделкой тоннелей[7], железобетонными, бетонными плитами, каменной кладкой или дорожной одеждой[8]. В случае увеличения скоростей с глубиной (как правило, при исследованиях с дневной поверхности) скорости поперечных волн в нижнем слое определяются по дисперсионным кривым псевдорэлеевских волн (см. рисунок). Этот способ широко используется практически и обоснован с точки зрения теории упругости.
Примечания
- Lord Rayleigh. On Waves Propagated along the Plane Surface of an Elastic Solid (англ.) // Proc. London Math. Soc. : journal. — 1885. — Vol. s1—17, no. 1. — P. 4—11.
- Викторов И. А., 1981, с. 11.
- Викторов И. А., 1981, с. 7.
- Викторов И. А., 1981, с. 8.
- Викторов И. А., 1981, с. 9.
- Викторов И. А., 1981, с. 10.
- Оценка свойств и состояния грунтов за обделкой транспортных тоннелей по данным 2D-сейсмотомографии. Бойко О. В. (недоступная ссылка). Дата обращения: 10 июля 2015. Архивировано 10 июля 2015 года.
- Определение физико-механических свойств и прочностных характеристик грунтов, перекрытых каменной кладкой, бетонными, железобетонными конструкциями и дорожной одеждой. (недоступная ссылка). Дата обращения: 10 июля 2015. Архивировано 9 июля 2015 года.
Литература
- Викторов И. А. Звуковые поверхностные волны в твердых телах. — М.: Наука, 1981. — 287 с.