Вершина кривой
Вершина кривой — точка кривой, в которой первая производная кривизны равна нулю[1]. Как правило, это локальный максимум или минимум кривизны[2] и некоторые авторы определяют вершину как экстремальную точку кривизны, то есть максимум или минимум кривизны[3]. Различие определений проявляется, например, когда вторая производная кривизны равна нулю.
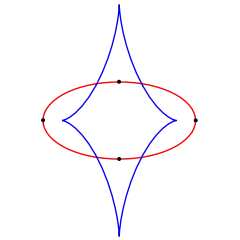
Примеры
Гипербола имеет две вершины по одной на каждой ветке. Эти вершины имеют наименьшее расстояние между двумя точками на гиперболе и лежат на главной оси. На параболе всего одна вершина и она лежит на оси симметрии[2]. У эллипса четыре вершины, две из них лежат на большой оси и две на малой[4].
На окружности, поскольку она имеет постоянную кривизну[5], любая точка является вершиной.
Точки перегиба и касания
Вершины — это точки, где кривая имеет касание порядка 3 с соприкасающейся окружностью в этой точке[6][3]. Обычно точки на кривой имеют с соприкасающейся окружностью касание второго порядка. Эволюта кривой обычно имеет касп, если кривая имеет вершину[3]. Могут случаться и другие особые точки в вершинах большего порядка, в которых порядок соприкосновения с соприкасающейся окружностью больше трёх[6], хотя обычно кривая не имеет вершин высокого порядка, в семействах кривых две обычные вершины могут слиться в вершину большего порядка, а затем исчезнуть.
Множество симметрии кривой имеет концы в каспах, соответствующих вершинам, а срединная ось, подмножество множества симметрии, также имеет концы в каспах.
Свойства
- Согласно теореме о четырёх вершинах любая замкнутая кривая должна иметь по меньшей мере четыре вершины[7].
- Если кривая зеркально симметрична, она имеет вершину в точке пересечения оси симметрии с кривой. Таким образом, понятие вершины кривой тесно связано оптическими точками — точками, в которых оптическая ось пересекает поверхность линзы.
Примечания
- Agoston, 2005, p. 570; Gibson, 2001, p. 126
- Gibson, 2001, p. 127
- Табачников С. Л., Фукс Д. Б. Математический дивертисмент. — МЦНМО, 2011.
- Agoston, 2005, p. 570; Gibson, 2001, p. 127
- 18.1. Определение кривизны и радиуса кривизны кривой
- Gibson, 2001, p. 126
- Agoston, 2005, Теорема 9.3.9, C. 570; Gibson, 2001, Section 9.3 «The Four Vertex Theorem», С. 133—136; Fuks & Tabachnikov, 2007, Теорема 10.3, С. 149
Ссылки
- Max K. Agoston. Computer Graphics and Geometric Modelling: Mathematics. — Springer, 2005. — ISBN 9781852338176.
- Табачников С.Л., Фукс Д.Б. Математический дивертисмент. — МЦНМО, 2011. — ISBN 978-5-94057-731-7.
- C. G. Gibson. Elementary Geometry of Differentiable Curves: An Undergraduate Introduction. — Cambridge University Press, 2001. — ISBN 9780521011075.
- Fuks, D. B. & Tabachnikov, Serge (2007), Mathematical Omnibus: Thirty Lectures on Classic Mathematics, American Mathematical Society, ISBN 9780821843161