Срединная ось

Срединная ось фигуры является геометрическим объектом, представляющим собой геометрическое место точек плоскости, равноудаленных от границы фигуры (то есть имеющих, по крайней мере, две ближайшие точки на границе фигуры).

Понятие срединной оси было впервые введено в 1967 году Х. Блюмом[1] при разработке методов анализа формы биологических объектов.

Алгоритмы построения срединной оси широко используются в задачах цифровой обработки изображений, анализа формы, распознавания образов, математического моделирования.

Срединная ось тесно связана со скелетом фигуры. Скелет и срединная ось плоской фигур являются одним и тем же объектом с практической точки зрения, а с формальной точки зрения отличаются лишь тем, что в скелет содержит точки границы, в которых она не дифференцируема и образует выпуклую вершину, в то время как срединная ось не содержит граничных точек вообще.

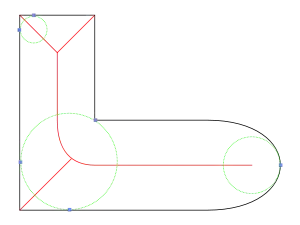
Определение

Пусть $\Omega$ — плоская фигура, то есть связное компактное множество точек плоскости, ограниченное конечным числом непересекающихся жордановых кривых, и $\Omega ^{c}$ — граница фигуры.

Обозначим $B(x)$ множество граничных точек $\Omega$ , ближайших к точке $x\in \Omega$ (в Евклидовой метрике): $B(x)=\{y\in \Omega ^{c}|d(x,y)=d(x,\Omega ^{c})\}$ .

Срединной осью плоской фигуры $\Omega$ называется множество $M_{\Omega }$ точек $x\in \Omega$ , имеющих, по крайней мере, две ближайшие граничные точки: $M_{\Omega }=\{x\in \Omega |Card(B(x))\geqslant 2\}$ .

В общем случае, срединная ось может быть аналогична определена для объекта произвольной размерности. В этом случае требуется, чтобы $\Omega$ являлось $n$ -мерным связным многообразием с краем.

Алгоритмы построения

Большинство алгоритмов построения срединной оси основаны на аппроксимации исходной фигуры многоугольной фигурой с требуемой степенью точности, построении диаграммы Вороного множества её вершин и отрезков и удалении из диаграммы Вороного некоторых дуг и отрезков.

Примечания

A transformation for extracting new descriptors of shape H. Blum, Models for the perception of speech and visual form, 1967

См. также

Множество раздела

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] A transformation for extracting new descriptors of shape H. Blum, Models for the perception of speech and visual form, 1967