Бидуга

Бидуга́ — гладкая плоская кривая, составленная из двух круговых дуг, меньших полной окружности. Одной из дуг может быть отрезок прямой. Бидуги были предложены [1] для геометрического моделирования (построения, аппроксимации) кривых с заданными граничными точками и касательными в них. В классе бидуг эта задача имеет целое семейство решений, и требует дополнительных условий для нахождения конкретных кривых. Таковыми могут быть задание кривизны или поворота одной из дуг, фиксированная длина кривой[2], требование минимизации скачка кривизны в точке сопряжения, и т. п.

Рис. 1. Примеры бидуг

У бидуги зависимость $k(s)$ кривизны от длины дуги монотонна (так как состоит из двух постоянных участков), поэтому бидуга является простейшей спиралью[3].

Примеры бидуг

На рис. 1 показаны шесть бидуг $AJB$ . Точки $A$ и $B$ — начальная и конечная точки кривой, $J$ (join) — точка гладкого сопряжения двух дуг.

Примеры 1-4 иллюстрируют короткие бидуги: они не пересекают дополнение хорды до бесконечной прямой, хотя могут пересекать саму хорду (бидуга 1). Обычно именно такие кривые являются объектами аппроксимации.

Примеры 5 и 6 иллюстрируют длинные бидуги: они пересекают дополнение хорды, то есть закручиваются вокруг одной из концевых точек.

У кривых 1, 2 и 6 точка $J$ является точкой перегиба: в ней кривизна меняет знак (- на + у кривых 1, 2 и + на - у кривой 6).

Кривые помещены в систему координат хорды ${\overrightarrow {AB}}$ длины $\;2c=|AB|$ , в которой координаты начальной и конечной точек равны $A=(-c,0),\;\;B=(c,0)$ .

Ориентированные углы наклонов касательных в точках $A$ и $B$ , измеренные относительно направления хорды ${\overrightarrow {AB}}$ , обозначены $\alpha$ и $\beta$ . Так, у бидуги 1 на рис. 1 $\;\alpha >0,\;\beta >0$ , а у бидуг 2-6 — $\;\alpha >0,\;\beta <0$ .

Описание семейства бидуг

Граничные касательные векторы у кривых 2-6 на рис. 1 одинаковы: $\alpha =100^{\circ },\quad \beta =-30^{\circ }.$ Эти кривые являются членами однопараметрического семейства бидуг с общими касательными на концах. Всё семейство показано на нижнем фрагменте рисунка 2.

Далее основные свойства семейства бидуг с общими касательными на концах приведены по материалам статьи[4]. Параметр семейства обозначен $p$ . Обозначение бидуги в виде ${\mathcal {B}}(p)$ подразумевает фиксацию констант, то есть ${\mathcal {B}}(p;\,\alpha ,\beta ,c)$ .

Рисунки 2, 3, 4 иллюстрируют такие семейства для различных пар $\{\alpha ,\beta \}.$

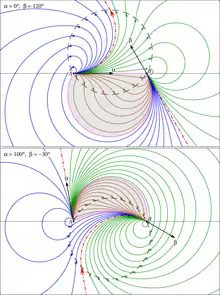Рис. 2. Семейства бидуг с общими касательными на концах (два примера)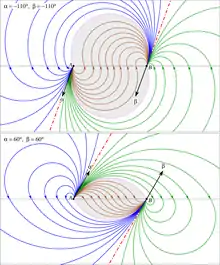

Рис. 3. Два семейства с общими (параллельными) касательными на концах: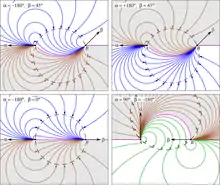

\alpha =\beta

Рис. 4. Семейства бидуг с

|\alpha |=\pi

или

|\beta |=\pi

Соотношения для углов и кривизн

Углы $\alpha$ и $\beta$ считаются определёнными в диапазоне ${\displaystyle [-\pi$ : $-\pi \leqslant \alpha \leqslant \pi$ , $-\pi \leqslant \beta \leqslant \pi$ . Построение бидуги возможно при

\qquad 0<|\alpha +\beta |<2\pi .\qquad (1)

Введём обозначения

\omega ={\frac {\alpha +\beta }{2}},\quad \gamma ={\frac {\alpha -\beta }{2}}

.

Неравенства (1) означают, что $\;\sin \omega \not =0$ .

Кривизна $k_{1}$ первой дуги $(AJ)$ и кривизна $k_{2}$ второй дуги $(JB)$ выражаются, как функции параметра семейства, следующими формулами:

k_{1}(p)={\frac {1}{c}}\left(-\sin \alpha -{\frac {\sin \omega }{p}}\right),\quad k_{2}(p)={\frac {1}{c}}\left(\sin \beta +p\sin \omega \right).

Пусть

$\theta _{1}$ и $L_{1}$ — поворот и длина дуги $AJ$ : $\theta _{1}=k_{1}L_{1}$ ;
$\theta _{2}$ и $L_{2}$ — поворот и длина дуги $JB$ : $\theta _{2}=k_{2}L_{2}$ .

Справедливы равенства

\theta _{1}(p)=2\arg \left(\mathrm {e} ^{-\mathrm {i} \alpha }+p^{-1}{\mathrm {e} ^{-\mathrm {i} \omega }}\right),\quad \theta _{2}(p)=2\arg \left(\mathrm {e} ^{\mathrm {i} \beta }+p\,\mathrm {e} ^{\mathrm {i} \omega }\right).

Геометрическое место точек сопряжения

Точки сопряжения $J$ двух дуг расположены на окружности

X_{J}(p)={\frac {c(p^{2}-1)}{p^{2}+2p\cos \gamma +1}},\quad Y_{J}(p)={\frac {2cp\sin \gamma }{p^{2}+2p\cos \gamma +1}},\quad -\infty \leqslant p\leqslant \infty .\qquad (2)

Эта окружность выходит из точки $A$ под углом $\gamma$ и проходит через точку $B.$ При $\gamma =0$ (то есть при $\alpha =\beta$ ) это прямая $AB$ (рис. 3). Бидуги семейства пересекают эту окружность под постоянным углом $-\omega$ .

Вектор касательной к бидуге в точке сопряжения есть $||\cos \tau _{{}_{J}},\,\sin \tau _{{}_{J}}||$ , где

\tau _{{}_{J}}(p)={-2}\operatorname {arctg} {\dfrac {p\sin {\frac {\alpha }{2}}+\sin {\frac {\beta }{2}}}{p\cos {\frac {\alpha }{2}}+\cos {\frac {\beta }{2}}}}.

Бидуга с минимальным скачком кривизны в точке сопряжения, $\min \left|k_{2}(p)-k_{1}(p)\right|,$ реализуется при $p=\pm 1;$ точка $J$ при этом лежит на оси ординат $(X_{J}=0).$

Вырожденные бидуги

В семействе бидуг можно выделить следующие вырожденные бидуги.

Бидуга ${\mathcal {B}}(0)$ : при $p\to 0$ точка сопряжения $J(p)$ бидуги $AJB$ стремится к точке $A$ , часть $AJ$ исчезает, превращаясь в бесконечный импульс кривизны. Бидуга вырождается в дугу окружности, опирающуюся на хорду $AB$ и имеющую с бидугами семейства общую касательную в конечной точке.
Бидуга ${\mathcal {B}}(\infty )$ : стремление $p\to \infty$ влечёт $J(p)\to B$ , часть $JB$ исчезает. Бидуга вырождается в дугу окружности, опирающуюся на хорду $AB$ и имеющую с бидугами семейства общую касательную в начальной точке.
Бидуга ${\mathcal {B}}(p^{\ast })$ , где
$\qquad p^{\ast }=\left\{{\begin{array}{lll}-{\dfrac {\sin \omega }{\sin \alpha }},\quad &{\text{если}}\;|\alpha |\geqslant |\beta |\quad (-\infty ,\;{\text{при}}\;|\alpha |=\pi ),\\-{\dfrac {\sin \beta }{\sin \omega }},\quad &{\text{если}}\;|\alpha |\leqslant |\beta |\quad (\;0,\;\;\;{\text{при}}\;|\beta |=\pi ),\end{array}}\right.$

представляет собой разрывную бидугу, проходящую через бесконечно удалённую точку плоскости. Всегда $p^{\ast }\leqslant 0$ , а неравенства (1) исключают одновременное равенство $|\alpha |=|\beta |=\pi$ .
На рисунках 2, 3 разрывные бидуги показаны красной штрих-пунктирной линией.

С учётом этих трёх вырожденных бидуг через любую точку плоскости с выколотыми полюсами $A$ и $B$ проходит единственная бидуга ${\mathcal {B}}(p)$ . Именно, через точку $(x,y)$ проходит бидуга с параметром

\qquad p(x,y)=\left\{{\begin{array}{ll}-{\dfrac {[(x+c)^{2}+y^{2}]\sin \omega }{(c^{2}-x^{2}-y^{2})\sin \alpha -2cy\cos \alpha }},\quad &{\text{если}}\quad \omega \,C(x,y)\leqslant 0,\\-{\dfrac {(c^{2}-x^{2}-y^{2})\sin \beta +2cy\cos \beta }{[(x-c)^{2}+y^{2}]\sin \omega }},\quad &{\text{если}}\quad \omega \,C(x,y)\geqslant 0,\end{array}}\right.

где $\;C(x,y)=(c^{2}-x^{2}-y^{2})\sin \gamma -2cy\cos \gamma$ .

Структура семейства

В семействе бидуг ${\mathcal {B}}(p;\,\alpha ,\beta ,c)$ выделим, в зависимости от значения параметра $p,$ следующие подсемейства невырожденных бидуг:

{\begin{array}{l}{\mathcal {B}}^{\,+}(p){:}\quad p\in (0;\infty );\\{\mathcal {B}}_{1}^{\,-}(p){:}\quad p\in (p^{\ast };0);\\{\mathcal {B}}_{2}^{\,-}(p){:}\quad p\in (-\infty ;p^{\ast });\\{\mathcal {B}}^{\,-}(p)={\mathcal {B}}_{1}^{\,-}(p)\cup {\mathcal {B}}_{2}^{\,-}(p)\end{array}}

(в[4], Property 2, подсемейства ${\mathcal {B}}^{\,+}$ и ${\mathcal {B}}^{\,-}$ названы, соответственно, main subfamily и complementary subfamily).

На рисунках 2, 3, 4 бидуги, принадлежащие подсемействам $\color {sienna}{\mathcal {B}}^{\,+}$ , $\color {blue}{\mathcal {B}}_{1}^{\,-}$ и $\color {green}{\mathcal {B}}_{2}^{\,-}$ показаны, соответственно, коричневым, синим и зелёным цветом.

Бидуги подсемейства ${\mathcal {B}}^{\,+}$ — короткие. Их кривизна либо возрастает (если $\omega >0$ ), либо убывает (если $\omega <0$ ):

$\operatorname {sgn}(k_{2}-k_{1})=\operatorname {sgn} \omega =\operatorname {sgn}(\alpha +\beta )$ (теорема В.Фогта для коротких спиралей).

Они заключены внутри линзы — области, ограниченной вырожденными бидугами ${\mathcal {B}}(0)$ и ${\mathcal {B}}(\infty )$ (на рисунках область линзы затемнена). Угловая ширина линзы (со знаком) равна $\alpha +\beta =2\omega$ . ГМТ (2) есть биссектриса линзы.

Бидуги подсемейства ${\mathcal {B}}^{\,-}$ имеют противоположный (по отношению к ${\mathcal {B}}^{\,+}$ ) характер монотонности кривизны.
Если $|\alpha |\not =\pi$ и $|\beta |\not =\pi$ , то бидуги этого подсемейства — длинные. Разрывная бидуга $\color {red}{\mathcal {B}}(p^{\ast })$ отграничивает друг от друга бидуги подсемейств ${\mathcal {B}}_{{\color {blue}1},{\color {green}2}}^{\,-}$ .

Подсемейство ${\mathcal {B}}_{1}^{\,-}$ пусто, если $p^{\ast }=0$ $(|\beta |=\pi ).$

Подсемейство ${\mathcal {B}}_{2}^{\,-}$ пусто, если $p^{\ast }=-\infty$ $(|\alpha |=\pi ).$

Переопределение граничных углов в кумулятивном смысле. Интегрирование натурального уравнения бидуги даёт непрерывную (кусочно-линейную) функцию $\tau (s)$ — угол наклона касательной к кривой. При таком определении, непрерывном, её значения могут выйти за пределы $\pm \pi$ , и значения на концах могут отличаться от $\alpha ,\beta$ на $\pm 2\pi .$ Определим, наряду с $\alpha ,\beta$ , кумулятивные версии граничных углов в виде ${\widetilde {\alpha }},{\widetilde {\beta }}$ , с учётом непрерывности $\tau (s).$ Поправка к углу $\alpha$ вносится, если бидуга совершает оборот вокруг точки $A,$ то есть пересекает луч $\{x<-c,\,y=0\}$ ; поправка к углу $\beta$ вносится, если бидуга совершает оборот вокруг точки $B$ (пересекая правое дополнение хорды до бесконечной прямой):

в подсемействе ${\mathcal {B}}^{\,+}$ : ${\widetilde {\alpha }}=\alpha ,\qquad \qquad \quad {\widetilde {\beta }}=\beta$ ;
в подсемействе ${\mathcal {B}}_{1}^{\,-}$ : ${\widetilde {\alpha }}=\alpha -2\pi \operatorname {sgn} \omega ,\;{\widetilde {\beta }}=\beta$ ;
в подсемействе ${\mathcal {B}}_{2}^{\,-}$ : ${\widetilde {\alpha }}=\alpha ,\qquad \qquad \quad {\widetilde {\beta }}=\beta -2\pi \operatorname {sgn} \omega$ .

Тогда полный поворот бидуги ${\mathcal {B}}(p)$ равен

\theta _{1}(p)+\theta _{2}(p)={\widetilde {\beta }}-{\widetilde {\alpha }},

а возрастание/убывание кривизны соответствует равенству

\operatorname {sgn}(k_{2}-k_{1})=\operatorname {sgn}({\widetilde {\alpha }}+{\widetilde {\beta }}).

Так, для бидуг с возрастающей кривизной, $k_{2}>k_{1}$ , имеем:

{\widetilde {\alpha }}>-\pi ,\quad {\widetilde {\beta }}>-\pi ,\quad 0<{\widetilde {\alpha }}+{\widetilde {\beta }}<2\pi .

Ссылки

Bolton, K. M. Biarc curves (англ.) // Computer-Aided Design. — 1975. — Vol. 7. — P. 89—92. — doi:10.1016/0010-4485(75)90086-X.
Сабитов И.Х., Словеснов А.В. Приближение плоских кривых круговыми дугами // Журнал вычислительной математики и математической физики. — 2010. — Т. 50, № 8. — С. 1347—1356.
Курносенко А.И. Общие свойства плоских спиральных кривых // Записки научных семинаров ПОМИ. — 2009. — Т. 353. — С. 93—115. — ISSN 0373-2703.
Kurnosenko, A. I. Biarcs and bilens (англ.) // Computer Aided Geometric Design. — 2013. — Vol. 30, no. 3. — P. 310—330. — doi:10.1016/j.cagd.2012.12.002.

Литература

Nutbourne, A. W.; Martin, R. R. Differential geometry applied to curve and surface design. Vol.1: Foundations (англ.). — Ellis Horwood, 1988. — ISBN 013211822X.

См. также

Теорема Фогта

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Bolton, K. M. Biarc curves (англ.) // Computer-Aided Design. — 1975. — Vol. 7. — P. 89—92. — doi:10.1016/0010-4485(75)90086-X.

[2] Сабитов И.Х., Словеснов А.В. Приближение плоских кривых круговыми дугами // Журнал вычислительной математики и математической физики. — 2010. — Т. 50, № 8. — С. 1347—1356.

[3] Курносенко А.И. Общие свойства плоских спиральных кривых // Записки научных семинаров ПОМИ. — 2009. — Т. 353. — С. 93—115. — ISSN 0373-2703.

[Kurnosenko2013-4] Kurnosenko, A. I. Biarcs and bilens (англ.) // Computer Aided Geometric Design. — 2013. — Vol. 30, no. 3. — P. 310—330. — doi:10.1016/j.cagd.2012.12.002.