Аксиома Плейфера

Аксиома Плейфера — это аксиома, которая может быть использована вместо пятого постулата Евклида (аксиомы параллельности):

Если дана прямая на плоскости и точка вне этой прямой, максимум одна прямая, параллельная данной прямой, может быть проведена через точку[1].

Исходное условие аксиомы Плейфера: прямая и точка вне прямой
Логическое следствие аксиомы Плейфера: вторая прямая, параллельная первой и проходящая через точку

Аксиома Плейфера эквивалентна аксиоме параллельности Евклида в контексте евклидовой геометрии[2]. Аксиома была названа именем шотландского математика Джона Плейфера. Фраза «максимум одна», это всё, что нужно, поскольку из остальных аксиом можно доказать, что хотя бы одна прямая существует. Утверждение часто записывается в виде, «существует одна и только одна параллельная». В «Началах» Евклида две прямые называются параллельными, если они не пересекаются и других описаний параллельных прямых не используется[3][4].

Аксиома используется не только в евклидовой геометрии, но и также в аффинной геометрии, в которой понятие параллельности является центральным. В условиях аффинной геометрии нужна более сильная форма аксиомы Плейфера (в которой «максимум одна» заменено на «одна и только одна»), поскольку аксиомы нейтральной геометрии не дают доказательство существования. Версия Плейфера аксиомы стала настолько популярна, что о ней говорят как об аксиоме параллельности Евклида[5], хотя она не является евклидовой версией аксиомы. Из аксиомы вытекает, что бинарное отношение параллельности прямых является серийным отношением.

История

Прокл (410–485 A.D.) ясно даёт утверждение аксиомы в комментариях к книге Евклида I.31 (Книга I, Утверждение 31)[6].

В 1785 Уильям Ладлэм высказал аксиому параллельности следующим образом[7]:

Две пересекающиеся в точке прямые не могут быть параллельны третьей прямой.

Это короткое выражение евклидовой параллельности заимствовал Плейфер в своей книге Elements of Geometry (Элементы геометрии, 1795), которая часто перепечатывалась. Он писал[8]:

Две пересекающиеся прямые не могут быть обе параллельны одной и той же третьей прямой.

Плейфер благодарил Ладлэма и других за упрощение утверждения Евклида. В дальнейшем точка пересечения двух прямых вышла на первое место и отрицание двух параллельных превратилось в единственность параллельных, проходящих через данную точку[9].

В 1883 Артур Кэли был президентом Британской Ассоциации и высказал такое мнение в своём обращении к Ассоциации[10]:

С моей точки зрения двенадцатая аксиома Евклида в форме Плейфера не требует доказательства, но является частью нашего понятия пространства, физического пространства нашего опыты, которое является представлением, лежащим в основе нашего жизненного опыта.

Когда Давид Гильберт написал свою книгу «Основания геометрии» (1899)[11], представляя новый набор аксиом для евклидовой геометрии, он использовал при обсуждении параллельных прямых аксиому в форме Плейфера, а не оригинальную версию Евклида[12].

Связь с пятым постулатом Евклида
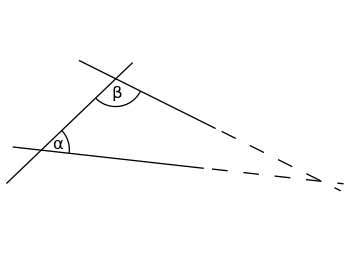
Если сумма внутренних углов α и β меньше 180°, две прямые, продолженные до бесконечности, пересекаются на этой стороне.

Аксиома параллельности Евклида утверждает:

Если отрезок пересекает две прямые, образуя два внутренних угла на одной стороне, дающих в сумме менее двух прямых углов, то две прямые, продолженные до бесконечности, пересекаются на стороне, на которой сумма углов меньше двух прямых углов[13].

Сложность этого утверждения по сравнению с формулировкой Плейфера ясно показывает причину популярности аксиомы Плейфера при обсуждении аксиомы параллельности.

В контексте абсолютной геометрии два утверждения эквивалентны, что означает, что одно утверждение может быть доказано из другого при наличии других аксиом геометрии. Утверждения не являются логически эквивалентными (что означало бы, что одно может быть доказано из другого только с помощью формальных логических выводов), поскольку, например, в сферической модели эллиптической геометрии одно утверждение верно, а другое ложно[14]. Логически эквивалентное утверждение верно во всех моделях, в которых оно интерпретируется.

Доказательства ниже предполагают, что все аксиомы абсолютной (нейтральной) геометрии выполняются.

Из пятого постулата Евклида вытекает аксиома Плейфера

Самый простой способ показать это — использовать теорему Евклида (эквивалентную пятому постулату), которая утверждает, что сумма углов треугольника равна двум прямым углам. Если дана прямая и точка P вне её, строим прямую t, перпендикулярную данной прямой и проходящую через точку P, а затем перпендикуляр к этому перпендикуляру через точку P. Эта прямая параллельна прямой , поскольку она не может пересечься с прямой и образовать треугольник, что говорится в утверждении 27 книги 1 в «Началах» Евклида[15]. Теперь видно, что никакой другой параллельной не существует. Если бы n была второй параллельной прямой через точку P, то n имела бы с прямой t острый угол (поскольку она не перпендикулярна), а при предположении верности гипотезы о пятом постулате n пересекалось бы с [16].

Из аксиомы Плейфера вытекает пятый постулат Евклида

Если из постулата Плейфера вытекает, что перпендикуляр к перпендикуляру параллелен исходной прямой, прямые из построения Евклида должны пересекаться. Следует доказать, что они будут пересекаться на стороне, на которой сумма углов меньше двух прямых углов, но это доказательство существенно сложнее[17].

Транзитивность параллельности

Утверждение 30 Евклида гласит: «Две прямые, каждая из которых параллельна третьей прямой, параллельны». Де Морган заметил[18], что это утверждение логически эквивалентно аксиоме Плейфера. Это замечание повторил Т. Л. Хит в 1908[19]. Аргументация де Моргана такова: Пусть X будет множеством различных пар пересекающихся прямых, а Y — множеством различных пар прямых, параллельных одной обще прямой. Если z представляет пару различных прямых, то утверждение,

Для всех z, если z находится в X, то z не находится в Y,

является аксиомой Плейфера (в терминах де Моргана, Никакой X не является Y) и ей логически эквивалентное противопоставление,

Для всех z, если z лежит в Y то z не лежит в X,

является утверждением Евклида I.30 о транзитивности параллельности (Никакой Y не является X).

Недавно импликация была перефразирована в терминах бинарного отношения параллельности прямых: В аффинной геометрии отношение считается отношением эквивалентности, что означает, что прямая принимается параллельной себе. Энди Лю[20] написал: «Пусть P будет точкой, не лежащей на прямой 2. Предположим, что как прямая 1, так и прямая 3 проходят через P и параллельны прямой 2. Согласно транзитивности они параллельны друг другу, а потому не могут иметь общую точку P. Отсюда следует, что это одна и та же прямая, что является аксиомой Плейфера.»

Примечания
  1. Playfair, 1846, с. 29.
  2. точнее, в контексте абсолютной геометрия.
  3. Euclid's elements, Book I, definition 23
  4. Heath, 1956, с. Vol. 1, p. 190.
  5. например, у Рафаэля Артци (Rafael Artzy (1965) Linear Geometry, page 202, Addison-Wesley)
  6. Heath, 1956, с. Vol. 1, p. 220.
  7. Ludlam, 1785, с. 145.
  8. Playfair, 1846, с. 11.
  9. Playfair, 1846, с. 291.
  10. Frankland, 1910, с. 31.
  11. Гильберт, 1923.
  12. Eves, 1963, с. 385-7.
  13. Phillips, 1826, с. 3.
  14. Henderson, Taimiņa, 2005, с. 139.
  15. Этот аргумент даёт больше, чем нужно для доказательства результата. Существуют доказательства параллельности, которые не используют эквивалентность пятому постулату.
  16. Greenberg, 1974, с. 107.
  17. Доказательство можно найти в книге Хита (Heath 1956, Vol. 1, p. 313)
  18. De Morgan, 1849.
  19. Heath, 1956, с. Vol. 1, p. 314.
  20. The College Mathematics Journal, 42(5):372

Литература
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.